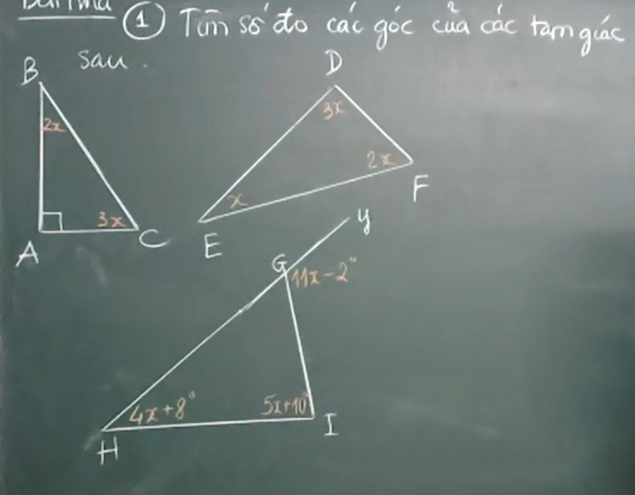
Làm hết hộ em với
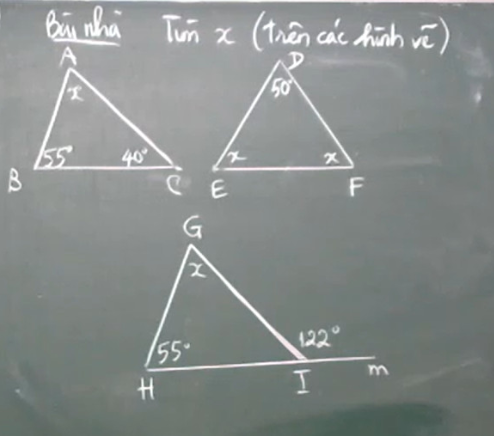
Làm hết hộ em với ạ
a: \(x=180^0-55^0-40^0=85^0\)
b: \(x=\dfrac{180^0-50^0}{2}=65^0\)
c: \(x=180^0-55^0-180^0+122^0=67^0\)
ai hộ mình với mỗi người làm 1 bài cũng đc ai làm mình tick hết đi mà các anh chị lớn cũng giúp em với em cảm ơn
ok bài gì vậy?
118:
80,71. 658,53. 613,72. 754.58
119:
a)55,24
b)238,932
c)613,545
d)563,552
120:
a)28,16
b)87,71
c)27,9
d)599,1
Làm hết sạch các câu bạn gửi à bạn
vậy tính ra thôi à

Làm hết hộ em nha, em cảm ơn ạ!
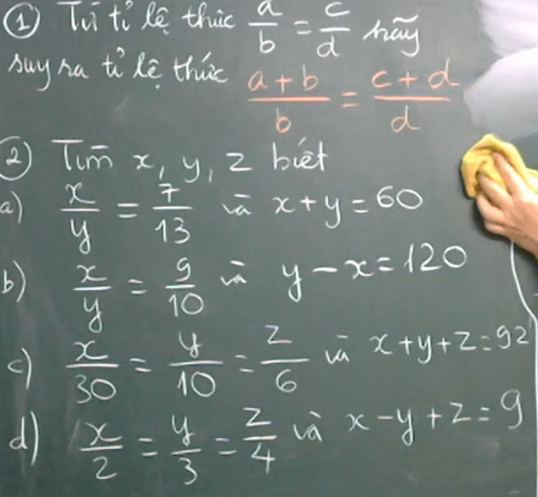
Làm hết hộ em nha!!!
Bài 2:
a) \(\dfrac{x}{y}=\dfrac{7}{13}\Rightarrow\dfrac{x}{7}=\dfrac{y}{13}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{7}=\dfrac{y}{13}=\dfrac{x+y}{7+13}=\dfrac{60}{20}=3\)
\(\dfrac{x}{7}=3\Rightarrow x=21\\ \dfrac{y}{13}=3\Rightarrow y=39\)
b) \(\dfrac{x}{y}=\dfrac{9}{10}\Rightarrow\dfrac{x}{9}=\dfrac{y}{10}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{9}=\dfrac{y}{10}=\dfrac{y-x}{10-9}=120\)
\(\dfrac{x}{9}=120\Rightarrow x=1080\\ \dfrac{y}{10}=120\Rightarrow y=1200\)
c) Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{30}=\dfrac{y}{10}=\dfrac{z}{6}=\dfrac{x+y+z}{30+10+6}=\dfrac{92}{46}=2\)
\(\dfrac{x}{30}=2\Rightarrow x=60\\ \dfrac{y}{10}=2\Rightarrow y=20\\ \dfrac{z}{6}=2\Rightarrow z=12\)
d)Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{x-y+z}{2-3+4}=\dfrac{9}{3}=3\)
\(\dfrac{x}{2}=3\Rightarrow x=6\\ \dfrac{y}{3}=3\Rightarrow y=9\\ \dfrac{z}{4}=3\Rightarrow z=12\)
Bài 1:
\(\dfrac{a+b}{b}=\dfrac{a}{b}+1\)
\(\dfrac{c+d}{d}=\dfrac{c}{d}+1\)
Mà \(\dfrac{a}{b}=\dfrac{c}{d};1=1\Rightarrow\dfrac{a}{b}+1=\dfrac{c}{d}+1\Rightarrow\dfrac{a+b}{b}=\dfrac{c+d}{d}\)

Làm hết hộ em nha em xin cảm ơn ạ
Bạn thể tự viết ra bởi vì mỗi người có những ý kiến khác nhau
Làm hết hộ em nha, em cảm ơn nhiều ạ!!
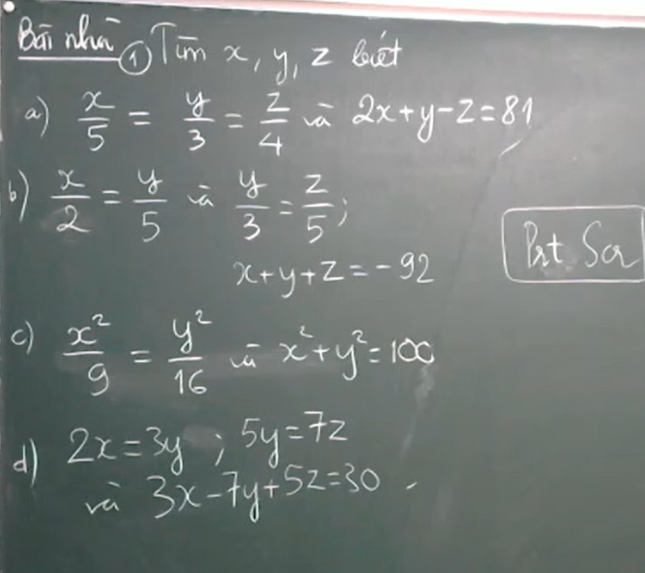
Làm hết hộ em nha em cảm ơn mọi người ạ
a) Ta có:
\(\dfrac{x}{5}=\dfrac{2x}{10}=\dfrac{y}{3}=\dfrac{z}{4}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta được:
\(\dfrac{2x}{10}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{2x+y-z}{10+3-4}=\dfrac{81}{9}=9\\ \Rightarrow\left\{{}\begin{matrix}x=9\cdot5=45\\y=9\cdot3=27\\z=9\cdot4=36\end{matrix}\right.\)
Vậy x = 45; y = 27; z = 36.
b) Ta có:
\(\dfrac{x}{2}=\dfrac{y}{5}\)\(\Rightarrow\dfrac{x}{6}=\dfrac{y}{15}\)
\(\dfrac{y}{3}=\dfrac{z}{5}\)\(\Rightarrow\dfrac{y}{15}=\dfrac{z}{25}\)
suy ra, \(\dfrac{x}{6}=\dfrac{y}{15}=\dfrac{z}{25}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{6}=\dfrac{y}{15}=\dfrac{z}{25}=\dfrac{x+y+z}{6+15+25}=-\dfrac{92}{46}=-2\\
\Rightarrow\left\{{}\begin{matrix}x=-2\cdot6=-12\\y=-2\cdot15=-30\\z=-2\cdot25=-50\end{matrix}\right.\)
Vậy x = -12; y = -30; z = -50.
c) Áp dụng tính chất dãy tỉ số bằng nhau, ta được:
\(\dfrac{x^2}{9}=\dfrac{y^2}{16}=\dfrac{x^2+y^2}{9+16}=4\\ \Rightarrow\left\{{}\begin{matrix}x^2=36\\y^2=64\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=6\\y=8\end{matrix}\right.\\\left\{{}\begin{matrix}x=-6\\y=8\end{matrix}\right.\\\left\{{}\begin{matrix}x=6\\y=-8\end{matrix}\right.\\\left\{{}\begin{matrix}x=-6\\y=-8\end{matrix}\right.\end{matrix}\right.\)
Vậy (x; y) \(\in\left\{\left(6;8\right);\left(-6;8\right);\left(6;-8\right);\left(-6;-8\right)\right\}\)
d), Ta có:
\(2x=3y\Rightarrow\dfrac{x}{3}=\dfrac{y}{2}\Rightarrow\dfrac{x}{21}=\dfrac{y}{14}\\ 5y=7z\Rightarrow\dfrac{y}{7}=\dfrac{z}{5}\Rightarrow\dfrac{y}{14}=\dfrac{z}{10}\\ \Rightarrow\dfrac{x}{21}=\dfrac{y}{14}=\dfrac{z}{10}\\ \Rightarrow\dfrac{3x}{63}=\dfrac{7y}{98}=\dfrac{5z}{50}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta được:
\(\dfrac{3x}{63}=\dfrac{7y}{98}=\dfrac{5z}{50}=\dfrac{3x-7y+5z}{63-98+50}=\dfrac{30}{15}=2\\
\Rightarrow\left\{{}\begin{matrix}x=2\cdot21=42\\y=2\cdot14=28\\z=2\cdot10=20\end{matrix}\right.\)
Vậy x = 42; y = 28; z = 20.
a: Ta có: \(\dfrac{x}{5}=\dfrac{y}{3}=\dfrac{z}{4}\)
nên \(\dfrac{2x}{10}=\dfrac{y}{3}=\dfrac{z}{4}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{2x}{10}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{2x+y-z}{10+3-4}=\dfrac{81}{9}=9\)
Do đó: x=45; y=27; z=36
b: Ta có: \(\dfrac{x}{2}=\dfrac{y}{5}\)
nên \(\dfrac{x}{6}=\dfrac{y}{15}\left(1\right)\)
Ta có: \(\dfrac{y}{3}=\dfrac{z}{5}\)
nên \(\dfrac{y}{15}=\dfrac{z}{25}\left(2\right)\)
Từ (1), (2) suy ra \(\dfrac{x}{6}=\dfrac{y}{15}=\dfrac{z}{25}\)
mà x+y+z=-92
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{6}=\dfrac{y}{15}=\dfrac{z}{25}=\dfrac{x+y+z}{6+15+25}=-\dfrac{92}{46}=-2\)
Do đó: x=-12; y=-30; z=-50
c: Ta có: \(\dfrac{x^2}{9}=\dfrac{y^2}{16}\)
mà \(x^2+y^2=100\)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x^2}{9}=\dfrac{y^2}{16}=\dfrac{x^2+y^2}{9+16}=\dfrac{100}{25}=4\)
Do đó: \(\left\{{}\begin{matrix}x^2=36\\y^2=64\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\in\left\{6;-6\right\}\\y\in\left\{8;-8\right\}\end{matrix}\right.\)
d: Ta có: 2x=3y
nên \(\dfrac{x}{3}=\dfrac{y}{2}\)
hay \(\dfrac{x}{21}=\dfrac{y}{14}\left(1\right)\)
Ta có: 5y=7z
nên \(\dfrac{y}{7}=\dfrac{z}{5}\)
hay \(\dfrac{y}{14}=\dfrac{z}{15}\left(2\right)\)
Từ (1), (2) suy ra \(\dfrac{x}{21}=\dfrac{y}{14}=\dfrac{z}{15}\)
hay \(\dfrac{3x}{63}=\dfrac{7y}{98}=\dfrac{5z}{75}\)
mà 3x-7y+5z=30
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{3x}{63}=\dfrac{7y}{98}=\dfrac{5z}{75}=\dfrac{3x-7y+5z}{63-98+75}=\dfrac{30}{40}=\dfrac{3}{4}\)
Do đó: \(\left\{{}\begin{matrix}x=\dfrac{63}{4}\\y=\dfrac{21}{2}\\z=\dfrac{45}{4}\end{matrix}\right.\)
 Làm hộ em vs ạ:'((, hết luôn nha
Làm hộ em vs ạ:'((, hết luôn nha
38 No, they don't
39 They can get a job or can go to college
40 They learn practical subjects like typing, cooking, mechanics, hairdressing
41 They take it at the end of the sixth form
I
42 The boy said he came from Thanh Hoa
43 We had to cancel the game because it was raining hard
44 She hasn't phoned her parents for five weeks
45 The highway will be completed in two months
46 I wish I had a big house
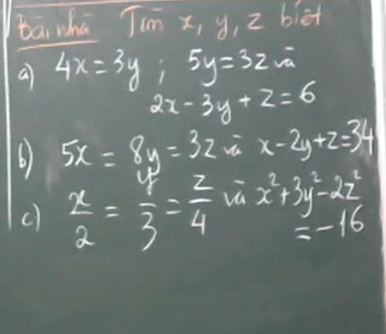
Làm hết hộ em nha! Em xin cảm ơn mọi người nhiều ạ!
Lời giải:
a.
$4x=3y\Rightarrow 20x=15y$
$5y=3z\Rightarrow 15y=9z$
$\Rightarrow 20x=15y=9z=t$
$\Rightarrow x=\frac{t}{20}; y=\frac{t}{15}; z=\frac{t}{9}$
Khi đó:
$2x-3y+z=\frac{2t}{20}-\frac{3t}{15}+\frac{t}{9}=5$
$\frac{t}{90}=6$
$t=540$
$x=\frac{540}{20}=27; y=\frac{540}{15}=36;z=\frac{540}{9}=60$
b. Đặt $5x=8y=3z=t$
$\Rightarrow x=\frac{t}{5}; y=\frac{t}{8}; z=\frac{t}{3}$
Khi đó:
$x-2y+z=34$
$\frac{t}{5}-\frac{2t}{8}+\frac{t}{3}=34$
$\frac{17}{60}t=34$
$t=120$
$x=\frac{120}{5}=24; y=\frac{120}{8}=15; z=\frac{120}{3}=40$
c.
Đặt $\frac{x}{2}=\frac{y}{3}=\frac{z}{4}=t$
$\Rightarrow x=2t; y=3t; z=4t$
Khi đó:
$x^2+3y^2-2z^2=-16$
$(2t)^2+3(3t)^2-2(4t)^2=-16$
$-t^2=-16$
$t^2=16$
$t=\pm 4$
Khi $t=4$ thì $x=2.4=8; y=3.4=12; z=4.4=16$
Khi $t=-4$ thì $x=-8; y=-12; z=-16$
b: Ta có: \(5x=8y=3z\)
\(\Leftrightarrow\dfrac{x}{\dfrac{1}{5}}=\dfrac{y}{\dfrac{1}{8}}=\dfrac{z}{\dfrac{1}{3}}\)
hay \(\dfrac{x}{\dfrac{1}{5}}=\dfrac{2y}{\dfrac{1}{4}}=\dfrac{z}{\dfrac{1}{3}}\)
mà x-2y+z=34
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{\dfrac{1}{5}}=\dfrac{2y}{\dfrac{1}{4}}=\dfrac{z}{\dfrac{1}{3}}=\dfrac{x-2y+z}{\dfrac{1}{5}-\dfrac{1}{4}+\dfrac{1}{3}}=\dfrac{34}{\dfrac{17}{60}}=120\)
Do đó: x=24; y=15; z=40