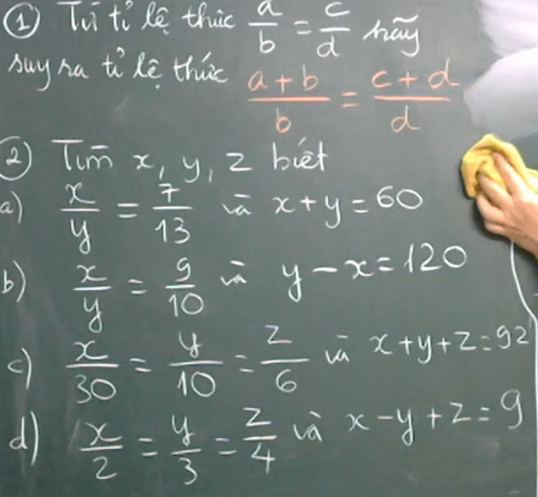Bài 2:
a) \(\dfrac{x}{y}=\dfrac{7}{13}\Rightarrow\dfrac{x}{7}=\dfrac{y}{13}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{7}=\dfrac{y}{13}=\dfrac{x+y}{7+13}=\dfrac{60}{20}=3\)
\(\dfrac{x}{7}=3\Rightarrow x=21\\ \dfrac{y}{13}=3\Rightarrow y=39\)
b) \(\dfrac{x}{y}=\dfrac{9}{10}\Rightarrow\dfrac{x}{9}=\dfrac{y}{10}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{9}=\dfrac{y}{10}=\dfrac{y-x}{10-9}=120\)
\(\dfrac{x}{9}=120\Rightarrow x=1080\\ \dfrac{y}{10}=120\Rightarrow y=1200\)
c) Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{30}=\dfrac{y}{10}=\dfrac{z}{6}=\dfrac{x+y+z}{30+10+6}=\dfrac{92}{46}=2\)
\(\dfrac{x}{30}=2\Rightarrow x=60\\ \dfrac{y}{10}=2\Rightarrow y=20\\ \dfrac{z}{6}=2\Rightarrow z=12\)
d)Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{x-y+z}{2-3+4}=\dfrac{9}{3}=3\)
\(\dfrac{x}{2}=3\Rightarrow x=6\\ \dfrac{y}{3}=3\Rightarrow y=9\\ \dfrac{z}{4}=3\Rightarrow z=12\)
Bài 1:
\(\dfrac{a+b}{b}=\dfrac{a}{b}+1\)
\(\dfrac{c+d}{d}=\dfrac{c}{d}+1\)
Mà \(\dfrac{a}{b}=\dfrac{c}{d};1=1\Rightarrow\dfrac{a}{b}+1=\dfrac{c}{d}+1\Rightarrow\dfrac{a+b}{b}=\dfrac{c+d}{d}\)
Bài 2:
a: Ta có: \(\dfrac{x}{y}=\dfrac{7}{13}\)
nên \(\dfrac{x}{7}=\dfrac{y}{13}\)
mà x+y=60
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{7}=\dfrac{y}{13}=\dfrac{x+y}{7+13}=3\)
Do đó: x=21; y=39
b: Ta có: \(\dfrac{x}{y}=\dfrac{9}{10}\)
nên \(\dfrac{x}{9}=\dfrac{y}{10}\)
mà y-x=120
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{9}=\dfrac{y}{10}=\dfrac{y-x}{10-9}=120\)
Do đó: x=1080; y=1200
c: Ta có: \(\dfrac{x}{30}=\dfrac{y}{10}=\dfrac{z}{6}\)
mà x+y+z=92
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{30}=\dfrac{y}{10}=\dfrac{z}{6}=\dfrac{x+y+z}{30+10+6}=2\)
Do đó: x=60; y=20; z=12
d: Ta có: \(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}\)
mà x-y+z=9
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{x-y+z}{2-3+4}=3\)
Do đó: x=6; y=9; z=12
Bài 1:
Ta có: \(\dfrac{a}{b}=\dfrac{c}{d}\)
nên \(\dfrac{a}{b}+1=\dfrac{c}{d}+1\)
hay \(\dfrac{a+b}{b}=\dfrac{c+d}{d}\)