Trên tia AM lấy điểm D sao cho DM = AM . Nối D với C . CM , tam giác MBA bằng tam giác MCD ( c . g . c )

Suy ra góc BAM bằng góc CDM , suy ra CD // BA suy ra BAC+ DCA  = 180 độ và góc BAC bằng góc DCA theo CM 2 tam giác trên suy ra

  BAC = DCA = 90 độ

Kết luận : Tam giác trên là tam giac vuông tại A

kết luận tam giác trên là tam giác vuông để làm j người ta cho sẵn rồi mà

giúp mik nhanh câu c dc khum ạ

2 câu kia mik xong r

cảm ơn các bạn

ΔABC vuông tại A có AM là trung tuyến

nên MA=MB

mà MA=AB

nên MA=AB=MB

=>ΔMAB đều

=>góc B=60 độ

=>góc C=90-60=30 độ

sin C=sin 30=1/2

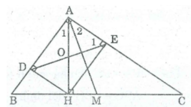
Ta có: AH ⊥ BC (gt) ⇒  ∠ (HAB) +  ∠ B = 90 0

Lại có:  ∠ B +  ∠ C =  90 0  (vì ∆ ABC có ∠A =  90 0 )

Suy ra  ∠ (HAB) =  ∠ C (1)

∆ ABC vuông tại A có AM là trung tuyến thuộc cạnh huyền BC

⇒ AM = MC = 1/2 BC (tính chất tam giác vuông)

⇒  ∆ MAC cân tại M ⇒  ∠ (MAC) =  ∠ C (2)

Từ (1) và (2) suy ra:  ∠ (HAB) =  ∠ (MAC)

Trên tia đối của tia MA, lấy điểm D sao cho MA=MD

Xét tứ giác ACDB có 

M là trung điểm của đường chéo BC

M là trung điểm của đường chéo AD

Do đó: ACDB là hình bình hành

Hình bình hành ACDB có \(\widehat{CAB}=90^0\)

nên ACDB là hình chữ nhật

Suy ra: BC=AD

mà \(AM=\dfrac{1}{2}AD\)

nên \(AM=\dfrac{1}{2}BC\)

áp dụng tính chất đường trung tuyến của tam giác vuông

=> AN=1/2BC

Để chứng minh rằng √2/AD = 1/AB + 1/AC, ta có thể sử dụng định lý phân giác trong tam giác vuông.

Vì tam giác ABC vuông tại A, nên ta có đường phân giác AD chia góc BAC thành hai góc bằng nhau.

Áp dụng định lý phân giác, ta có:

AB/BD = AC/CD

Từ đó, ta có:

AB/AD + AC/AD = AB/BD + AC/CD

= (AB + AC)/(BD + CD)

= (AB + AC)/BC

= 1/BC (vì tam giác ABC vuông tại A)

Vậy, ta có:

1/AD = 1/AB + 1/AC

√2/AD = √2/AB + √2/AC

Vậy, chứng minh đã được hoàn thành.

Để chứng minh rằng nếu 1/ah^2 + 1/am^2 = 2/ad^2, ta cần có thông tin chi tiết về tam giác ABC và các điều kiện đi kèm.

2/AD^2=(căn 2/AD)^2

=(1/AB+1/AC)^2

\(=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}+2\cdot\dfrac{1}{AB\cdot AC}\)

\(=\dfrac{1}{AH^2}+2\cdot\dfrac{1}{AH\cdot BC}\)

\(=\dfrac{1}{AH^2}+\dfrac{1}{AM^2}\)