Để khảo sát chuyển động ném ngang, ta chọn tọa độ đề - các như thế nào là thích hợp nhất? Nêu cách phân tích chuyển động ném ngang thành hai chuyển động thành phần theo hai trục của hệ tọa độ đó.

Những câu hỏi liên quan
Để khảo sát chuyển động ném ngang, ta chọn hệ tọa độ Đề - các như thế nào là thích hợp nhất? Nêu cách phân tích chuyển động ném ngang thành hai chuyển động thành phần theo hai trục của hệ tọa độ đó.
Để khảo sát chuyển động ném ngang, ta chọn hệ tọa độ Đề - các gồm 2 trục, trục Ox nằm ngang hướng theo vecto v0 ban đầu. Trục Oy thẳng đứng chiếu từ trên xuống, gốc tọa độ O trùng vị trí ném.
Gọi Mx và My là hình chiếu của chuyển động M lên hai trục Ox và Oy khảo sát chuyển động của Mx và My và tổng hợp lại được chuyển động của M.
Áp dụng định luật II Niu-tơn để lập các phương trình cho hai chuyển động thành phần của chuyển động ném ngang.
– Tổng hợp hai chuyển động thành phần để được chuyển động tổng hợp
– Vẽ được (một cách định tính) quỹ đạo parabol của một vật bị ném ngang.
Đúng 0
Bình luận (0)
Xét chuyển động ném ngang của một chất điểm M có gốc tọa độ O tại vị trị ném và hệ trục tọa độ Oxy (Ox nằm ngang; Oy đứng thẳng) nằm trong mặt phẳng quỹ đạo của M. Gọi
M
x
là hình chiếu của M trên phương Ox. Chuyển động của
M
x
là: A. Thẳng nhanh dần đều. B. Thẳng biến đổi đều. C. Thẳng đều. D. Rơi tự do.
Đọc tiếp
Xét chuyển động ném ngang của một chất điểm M có gốc tọa độ O tại vị trị ném và hệ trục tọa độ Oxy (Ox nằm ngang; Oy đứng thẳng) nằm trong mặt phẳng quỹ đạo của M. Gọi M x là hình chiếu của M trên phương Ox. Chuyển động của M x là:
A. Thẳng nhanh dần đều.
B. Thẳng biến đổi đều.
C. Thẳng đều.
D. Rơi tự do.
Chọn đáp án C.
Chuyển động ném ngang, theo phương Ox chất điểm chuyển động tahwngr đều, theo phương Oy chất điểm rơi tự do.
Đúng 0
Bình luận (0)
Xét chuyển động ném ngang của một chất điểm M có gốc tọa độ O tại vị trị ném và hệ trục tọa độ Oxy (Ox nằm ngang; Oy đứng thẳng) nằm trong mặt phẳng quỹ đạo của M. Gọi
M
x
là hình chiếu của M trên phương Ox. Chuyển động của
M
x
là A. Thẳng nhanh dần đều. B. Thẳng biến đổi đều. C. Thẳng đều. D. Rơi tự do
Đọc tiếp
Xét chuyển động ném ngang của một chất điểm M có gốc tọa độ O tại vị trị ném và hệ trục tọa độ Oxy (Ox nằm ngang; Oy đứng thẳng) nằm trong mặt phẳng quỹ đạo của M. Gọi M x là hình chiếu của M trên phương Ox. Chuyển động của M x là
A. Thẳng nhanh dần đều.
B. Thẳng biến đổi đều.
C. Thẳng đều.
D. Rơi tự do
Chọn C
Chuyển động ném ngang, theo phương Ox chất điểm chuyển động tahwngr đều, theo phương Oy chất điểm rơi tự do
Đúng 0
Bình luận (0)
Viết các chương trình của hai chuyển động thành phần của chuyển động ném ngang và cho biết tính chất của mỗi chuyển động thành phần.
Chuyển động thành phần theo trục Ox là chuyển động thẳng đều với các phương trình:
ax = 0
vx = vo
x = vot
Chuyển động thành phần theo trục Oy là chuyển động rơi tự do với các phương trình :
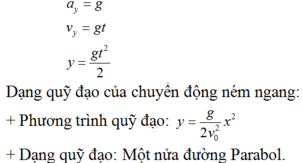
Đúng 0
Bình luận (0)
Viết các phương trình của hai chuyển động thành phần của chuyển động ném ngang và cho biết tính chất của mỗi chuyển động thành phần.
- Chuyển động thành phần theo trục Ox là chuyển động thẳng đều với các phương trình
\(a_x=0;v_x=v_0;x=v_0t\)
- Chuyển động thành phần theo trục Oy là chuyển động rơi tự do với các phương trình:
\(a_y=g;v_y=gt;y=\dfrac{1}{2}gt^2\)
Đúng 0
Bình luận (0)
từ độ cao cách mặt đất 10m,1 vật được ném theo phương ngang với vận tốc đấu 15m/s.a,lập phương trình chuyển động theo phương ngang và phương thẳng đứng ,chọn gốc tọa độ tại vị trí ném.b,tìm tầm ném xa của vậtc,tìm vận tốc khi chạm đất .Khi chạm đất phương chuyển động của vật hợp với phương thẳng đứng 1 góc bao nhiêud,khi đến vị trí cách mặt đất 5m,vận tốc của vạt là bao nhiêue,khi vật đến vị trí mà phương chuyển động hợp với phương thẳng đứng góc 45 độ thì vận tốc của vật là bao nhiêu.Tìm đô cao...
Đọc tiếp
từ độ cao cách mặt đất 10m,1 vật được ném theo phương ngang với vận tốc đấu 15m/s.
a,lập phương trình chuyển động theo phương ngang và phương thẳng đứng ,chọn gốc tọa độ tại vị trí ném.
b,tìm tầm ném xa của vật
c,tìm vận tốc khi chạm đất .Khi chạm đất phương chuyển động của vật hợp với phương thẳng đứng 1 góc bao nhiêu
d,khi đến vị trí cách mặt đất 5m,vận tốc của vạt là bao nhiêu
e,khi vật đến vị trí mà phương chuyển động hợp với phương thẳng đứng góc 45 độ thì vận tốc của vật là bao nhiêu.Tìm đô cao của vật ở vị trí này.
giúp mình vs mình cần rất gấp mình cần lúc 7h
1. Tìm hiểu bằng lí thuyếtVận dụng những kiến thức đã học về chuyển động ném để dự đoán về:- Để ném ngang một vật đạt tầm bay xa lớn nhất thì phải chọn độ cao như thế nào?- Để ném xiên một vật đạt tầm bay xa lớn nhất thì phải chọn góc ném như thế nào?2. Lập phương án làm thí nghiệm để kiểm tra dự đoán.3. Thực hiện thí nghiệm, rút ra kết luận.4. Viết báo cáo về kết quả tìm được.5. Trình bày báo cáo trước lớp.
Đọc tiếp
1. Tìm hiểu bằng lí thuyết
Vận dụng những kiến thức đã học về chuyển động ném để dự đoán về:
- Để ném ngang một vật đạt tầm bay xa lớn nhất thì phải chọn độ cao như thế nào?
- Để ném xiên một vật đạt tầm bay xa lớn nhất thì phải chọn góc ném như thế nào?
2. Lập phương án làm thí nghiệm để kiểm tra dự đoán.
3. Thực hiện thí nghiệm, rút ra kết luận.
4. Viết báo cáo về kết quả tìm được.
5. Trình bày báo cáo trước lớp.
1. Tìm hiểu bằng lí thuyết
- Để ném ngang một vật đạt tầm bay xa lớn nhất thì phải chọn độ cao lớn nhất.
- Để ném xiên một vật đạt tầm xa lớn nhất thì phải chọn góc ném
2. Lập phương án thí nghiệm
- Kiểm chứng kết quả ném ngang một vật đạt tầm bay xa lớn nhất thì phải chọn độ cao lớn nhất học sinh có thể tham khảo phương án thí nghiệm ở phần Hoạt động 1 trang 51 SGK Vật Lí 10.
- Kiểm chứng ném xiên một vật đạt tầm xa lớn nhất thì phải chọn góc ném α = 45° ta sẽ sử dụng một mặt phẳng nghiêng có độ nghiêng thay đổi được (mục đích thay đổi góc nghiêng), dùng một nam châm có gắn công tắc (giống như ở thí nghiệm kiểm chứng sự rơi tự do), viên bi sắt. Viên bi sắt được gắn vào nam châm, đặt ở khoảng giữa mặt phẳng nghiêng, bấm công tắc để viên bi bắn ra theo mặt phẳng nghiêng. Đo các kết quả tầm xa với các góc khác nhau
3. Học sinh tự viết ghi kết quả
Đúng 2
Bình luận (0)
Một thùng hàng trọng lượng 500 N đang trượt xuống dốc. Mặt dốc tạo với phương ngang một góc 30,00. Chọn hệ tọa độ vuông góc xOy sao cho trục Ox theo hướng chuyển động của thùng.a) Vẽ giản đồ vectơ lực tác dụng lên thùng.b) Tính các thành phần của trọng lực theo các trục tọa độ vuông góc.c) Giải thích tại sao lực pháp tuyến của dốc lên thùng hàng không có tác dụng kéo thùng hàng xuống dốc.d) Xác định hệ số ma sát trượt giữa mặt dốc và thùng hàng nếu đo được gia tốc chuyển động của thùng là 2,00m...
Đọc tiếp
Một thùng hàng trọng lượng 500 N đang trượt xuống dốc. Mặt dốc tạo với phương ngang một góc 30,00. Chọn hệ tọa độ vuông góc xOy sao cho trục Ox theo hướng chuyển động của thùng.
a) Vẽ giản đồ vectơ lực tác dụng lên thùng.
b) Tính các thành phần của trọng lực theo các trục tọa độ vuông góc.
c) Giải thích tại sao lực pháp tuyến của dốc lên thùng hàng không có tác dụng kéo thùng hàng xuống dốc.
d) Xác định hệ số ma sát trượt giữa mặt dốc và thùng hàng nếu đo được gia tốc chuyển động của thùng là 2,00m/s2. Bỏ qua lực cản của không khí lên thùng.
Một thùng hàng trọng lượng 500 N đang trượt xuống dốc. Mặt dốc tạo với phương ngang một góc 30,0^o. Chọn hệ tọa độ vuông góc xOy sao cho trục Ox theo hướng chuyển động của thùng.a) Vẽ giản đồ vectơ lực tác dụng lên thùng.b) Tính các thành phần của trọng lực theo các trục tọa độ vuông góc.c) Giải thích tại sao lực pháp tuyến của dốc lên thùng hàng không có tác dụng kéo thùng hàng xuống dốc.d) Xác định hệ số ma sát trượt giữa mặt dốc và thùng hàng nếu đo được gia tốc chuyển động của thùng là 2,00m...
Đọc tiếp
Một thùng hàng trọng lượng 500 N đang trượt xuống dốc. Mặt dốc tạo với phương ngang một góc \(30,0^o\). Chọn hệ tọa độ vuông góc xOy sao cho trục Ox theo hướng chuyển động của thùng.
a) Vẽ giản đồ vectơ lực tác dụng lên thùng.
b) Tính các thành phần của trọng lực theo các trục tọa độ vuông góc.
c) Giải thích tại sao lực pháp tuyến của dốc lên thùng hàng không có tác dụng kéo thùng hàng xuống dốc.
d) Xác định hệ số ma sát trượt giữa mặt dốc và thùng hàng nếu đo được gia tốc chuyển động của thùng là \(2,00m\)/s2. Bỏ qua lực cản của không khí lên thùng.
a)
Giản đồ vectơ các lực tác dụng lên thùng hàng:

b)
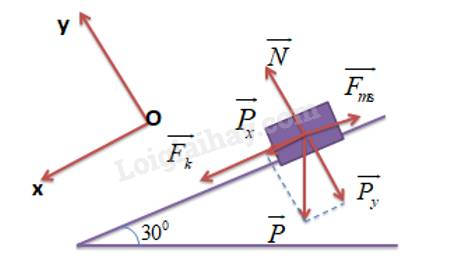
Ta có:
\({P_x} = P.\sin \alpha = 500.\sin {30^0} = 250N\)
\({P_y} = P.\cos \alpha = 500.\cos {30^0} = 500.\frac{{\sqrt 3 }}{2} = 250\sqrt 3 N\)
c)
Lực pháp tuyến của dốc lên thùng hàng không có tác dụng kéo thùng hàng xuống dốc vì nó cân bằng với thành phần \(\overrightarrow {{P_y}} \) của trọng lực.
d)
Chiếu các lực tác dụng lên trục Ox ta được:
\({F_k} - {F_{ms}} = ma \Leftrightarrow {F_k} - \mu N = ma\) (1)
Chiếu các lực tác dụng lên trục Oy ta được:
\(N - P.\cos \alpha = 0 \Leftrightarrow N = P.\cos \alpha = 250\sqrt 3 N\) (2)
Thay vào (1) ta được:
\(250 - \mu .250\sqrt 3 = \frac{{500}}{{10}}.2,00\)
\( \Leftrightarrow \mu = \frac{{150}}{{250\sqrt 3 }} = \frac{{\sqrt 3 }}{5} \approx 0,346\)
Vậy hệ số ma sát trượt giữa mặt dốc và thùng hàng là 0,346.
Đúng 0
Bình luận (0)










