Pi là số nguyên tố
thỏa mãn
\(\sum\limits^7_1P_i^2=P^2_8\)
Tìm Pi
Những câu hỏi liên quan
Chứng minh:
a)
\(\sum\limits^n_{i=1}cos\dfrac{2\left(i-1\right)\pi}{n}=0\)
b) \(\sum\limits^n_{i=1}sin\dfrac{2\left(i-1\right)\pi}{n}=0\)
Tìm lim un với un=\(\sum\limits^n_{k=1}sin^k\alpha\) (α≠\(\dfrac{\pi}{2}\) +kπ, k ϵ Z)
Cho hàm số f(x) liên tục trên \([-\Pi;\Pi]\)
Chứng minh: \(\int\limits^{\Pi}_0x.f\left(sinx\right)dx=\dfrac{\Pi}{2}\int\limits^{\Pi}_0f\left(sinx\right)dx\)
Este E (đơn chức, mạch hở, phân tử chứa hai liên kết pi) có tỉ lệ khối lượng các nguyên tố mC : mH = 8 : 1. Số đồng phân cấu tạo của E thỏa mãn là
A. 5.
B. 4.
C. 2.
D. 3.
Chọn đáp án A
Dùng phương pháp định tính phân tích: mC : mH = 8 : 1 ⇄ nC : nH = 2 : 3.
E là este đơn chức, mạch hở và phân tử chứa 2 liên kết π, E có dạng C2mH3mO2.
Dựa vào công thức tổng quát của este đơn chức là CnH2n + 2 – 2πO2
||→ có phương trình: 3m = 2 × 2m + 2 – 2 × 2 → giải ra m = 2.
||→ E là C4H6O2. Các đồng phân cấu tạo của E thỏa mãn gồm:
Đúng 0
Bình luận (0)
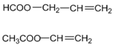
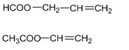
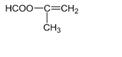
\(\sum\limits^{\infty}_{n=1}\left(n+4\right)^n\cdot sin\left(\dfrac{\Pi}{5^n}\right)\)
Hãy chỉ ra kết quả nào dưới đây đúng :
a) intlimits^{dfrac{pi}{2}}_0sin xdx+intlimits^{dfrac{3pi}{2}}_{dfrac{pi}{2}}sin xdx+intlimits^{2pi}_{dfrac{3pi}{2}}sin xdx0
b) intlimits^{dfrac{pi}{2}}_0left(sqrt[3]{sin x}-sqrt[3]{cos x}right)dx0
c) intlimits^{dfrac{1}{2}}_{-dfrac{1}{2}}lndfrac{1-x}{1+x}dx0
d) intlimits^2_0left(dfrac{1}{1+x+x^2+x^3}+1right)dx0
Đọc tiếp
Hãy chỉ ra kết quả nào dưới đây đúng :
a) \(\int\limits^{\dfrac{\pi}{2}}_0\sin xdx+\int\limits^{\dfrac{3\pi}{2}}_{\dfrac{\pi}{2}}\sin xdx+\int\limits^{2\pi}_{\dfrac{3\pi}{2}}\sin xdx=0\)
b) \(\int\limits^{\dfrac{\pi}{2}}_0\left(\sqrt[3]{\sin x}-\sqrt[3]{\cos x}\right)dx=0\)
c) \(\int\limits^{\dfrac{1}{2}}_{-\dfrac{1}{2}}\ln\dfrac{1-x}{1+x}dx=0\)
d) \(\int\limits^2_0\left(\dfrac{1}{1+x+x^2+x^3}+1\right)dx=0\)
18 tháng 9 2023 lúc 14:01
Cho \(a,b,c>0\) thỏa mãn \(\sum a^2+\left(\sum a\right)^2\le4\). Tìm giá trị nhỏ nhất của biểu thức \(S=\sum\limits^{ }_{cyc}\dfrac{ab+1}{\left(a+b\right)^2}\)
Tính các tích phân sau :
a) intlimits^1_0left(y^3+3y^2-2right)dy
b) intlimits^4_1left(t+dfrac{1}{sqrt{t}}-dfrac{1}{t^2}right)dt
c) intlimits^{dfrac{pi}{2}}_0left(2cos x-sin2xright)dx
d) intlimits^1_0left(3^s-2^sright)^2ds
e) intlimits^{dfrac{pi}{3}}_0cos3xdx+intlimits^{dfrac{3pi}{2}}_0cos3xdx+intlimits^{dfrac{5pi}{2}}_{dfrac{3pi}{2}}cos3xdx
g) intlimits^3_0left|x^2-x-2right|dx
h) intlimits^{dfrac{5pi}{4}}_{pi}dfrac{sin x-cos x}{sqrt{1+sin2x}}dx
i) intlimits^4_0dfrac{4x-1}{sqrt{2x+1}+2}dx
Đọc tiếp
Tính các tích phân sau :
a) \(\int\limits^1_0\left(y^3+3y^2-2\right)dy\)
b) \(\int\limits^4_1\left(t+\dfrac{1}{\sqrt{t}}-\dfrac{1}{t^2}\right)dt\)
c) \(\int\limits^{\dfrac{\pi}{2}}_0\left(2\cos x-\sin2x\right)dx\)
d) \(\int\limits^1_0\left(3^s-2^s\right)^2ds\)
e) \(\int\limits^{\dfrac{\pi}{3}}_0\cos3xdx+\int\limits^{\dfrac{3\pi}{2}}_0\cos3xdx+\int\limits^{\dfrac{5\pi}{2}}_{\dfrac{3\pi}{2}}\cos3xdx\)
g) \(\int\limits^3_0\left|x^2-x-2\right|dx\)
h) \(\int\limits^{\dfrac{5\pi}{4}}_{\pi}\dfrac{\sin x-\cos x}{\sqrt{1+\sin2x}}dx\)
i) \(\int\limits^4_0\dfrac{4x-1}{\sqrt{2x+1}+2}dx\)
Câu nào mình biết thì mình làm nha.
1) Đổi thành \(\dfrac{y^4}{4}+y^3-2y\) rồi thế số.KQ là \(\dfrac{-3}{4}\)
2) Biến đổi thành \(\dfrac{t^2}{2}+2\sqrt{t}+\dfrac{1}{t}\) và thế số.KQ là \(\dfrac{35}{4}\)
3) Biến đổi thành 2sinx + cos(2x)/2 và thế số.KQ là 1
Đúng 0
Bình luận (0)
Bài tập 1: Tính.
a, \(\int\limits^{\dfrac{\pi}{2}}_0\left(2-x\right).sinxdx\)
b, \(\int\limits^{\pi}_0sin2x.cos^22xdx\)
c, \(\int\limits^1_0x.e^x.dx\)
a.
Đặt \(\left\{{}\begin{matrix}u=2-x\\dv=sinxdx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=-dx\\v=-cosx\end{matrix}\right.\)
\(\Rightarrow I=\left(x-2\right).cosx|^{\dfrac{\pi}{2}}_0-\int\limits^{\dfrac{\pi}{2}}_0cosx.dx=2-1=1\)
b. Đặt \(cos2x=t\Rightarrow-2sin2x.dx=dt\Rightarrow sin2xdx=-\dfrac{1}{2}dt\)
\(\left\{{}\begin{matrix}x=0\Rightarrow t=1\\x=\pi\Rightarrow t=1\end{matrix}\right.\)
\(\Rightarrow I=\int\limits^1_1-\dfrac{1}{2}.t^2dt=0\) (hai cận bằng nhau thì tích phân bằng 0 khỏi tính dài dòng)
c. Đặt \(\left\{{}\begin{matrix}u=x\\dv=e^xdx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=dx\\v=e^x\end{matrix}\right.\)
\(I=x.e^x|^1_0-\int\limits^1_0e^xdx=\left(x.e^x-e^x\right)|^1_0=1\)
Đúng 0
Bình luận (0)