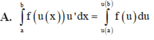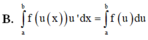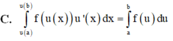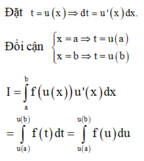Cho ví dụ về một hàm số liên tục trên (a; b] và trên (b;c) nhưng không liên tục trên (a; c) ?

Những câu hỏi liên quan
Cho ví dụ về một hàm số liên tục trên (a; b] và trên (b; c) nhưng không liên tục trên (a; c)
Xét hàm số
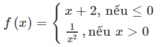
- Trường hợp x ≤ 0
f(x) = x + 2 là hàm đa thức, liên tục trên R nên nó liên tục trên (-2; 0]
- Trường hợp x > 0
f ( x ) = 1 / x 2 là hàm số phân thức hữu tỉ nên liên tục trên (2; 0) thuộc tập xác định của nó.
Như vậy f(x) liên tục trên (-2; 0] và trên (0; 2)
Tuy nhiên, vì 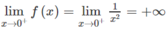 nên hàm số f(x) không cógiới hạn hữu hạn tại x = 0. Do đó, nó không liên tục tại x = 0. Nghĩa là không liên tục trên (-2; 2)
nên hàm số f(x) không cógiới hạn hữu hạn tại x = 0. Do đó, nó không liên tục tại x = 0. Nghĩa là không liên tục trên (-2; 2)
Đúng 0
Bình luận (0)
Cho hàm số y=f(x) liên tục trên đoạn [a; b]. Nếu f(a).f(b) > 0 thì phương trình f(x) = 0 có nghiệm hay không trong khoảng (a; b)? Cho ví dụ minh hoạ.
Nếu hàm số y = f(x) liên tục trên đoạn [a; b] và f(a).f(b) > 0 thì phương trình f(x) = 0 có thể có nghiệm hoặc vô nghiệm trong khoảng (a; b)
Ví dụ minh hoạ :
- f ( x ) = x 2 − 1 liên tục trên đoạn [−2;2], f(−2).f(2) = 9 > 0
Phương trình x 2 – 1 = 0 có nghiệm x = 1 hoặc x = -1 trong khoảng (-2; 2)
- f ( x ) = x 2 + 1 liên tục trên đoạn [-1; 1] và f(−1).f(1) = 4 > 0. Còn phương trình x 2 + 1 = 0 lại vô nghiệm trong khoảng (-1; 1)
Đúng 0
Bình luận (0)
Ví dụ 1:Cho hàm số (fx) left{{}begin{matrix}x^2-5xx^3-4x-1end{matrix}right.khi x-1 và x-1. Kết luận nào sau đây không đúng:A. H/s liên tục tại x -1B. H/s liên tục tại x1C. H/s liên tục tại x-3D. H/s liên tục tại x3Ví dụ 2:Cho hàm số f(x) dfrac{2x-1}{x^3-4x}Kết luận nào sau đây đúng:A. H/s liên tục tại x-2B. H/s liên tục tại x0C. H/s liên tục tại x0,5D. H/s liên tục tại x2Ví dụ 3:Cho f(x) dfrac{sqrt{x+2}-sqrt{2-x}}{x}Kết luận nào sau đây đúng?A. 0B. 1C. dfrac{1}{2}D. dfrac{1}{2sqrt{2}}Ví dụ 4:...
Đọc tiếp
Ví dụ 1:
Cho hàm số (fx) = \(\left\{{}\begin{matrix}x^2-5x\\x^3-4x-1\end{matrix}\right.\)khi x>-1 và x<-1.
Kết luận nào sau đây không đúng:
A. H/s liên tục tại x= -1
B. H/s liên tục tại x=1
C. H/s liên tục tại x=-3
D. H/s liên tục tại x=3
Ví dụ 2:
Cho hàm số f(x) = \(\dfrac{2x-1}{x^3-4x}\)
Kết luận nào sau đây đúng:
A. H/s liên tục tại x=-2
B. H/s liên tục tại x=0
C. H/s liên tục tại x=0,5
D. H/s liên tục tại x=2
Ví dụ 3:
Cho f(x) = \(\dfrac{\sqrt{x+2}-\sqrt{2-x}}{x}\)
Kết luận nào sau đây đúng?
A. 0
B. 1
C. \(\dfrac{1}{2}\)
D. \(\dfrac{1}{2\sqrt{2}}\)
Ví dụ 4:
Cho hàm số f(x)= \(\left\{{}\begin{matrix}3x-5\\ax-1\end{matrix}\right.\)khi x≤-2 và x>-2
Với giá trị nào của a thì hàm số f(x) liên tục tại x=-2?
A. a=-5
B, a=0
C. a=5
D. a=6
1. Hàm không liên tục tại \(x=-1\) nên đáp án A sai
2. Hàm liên tục tại \(x=0,5\)
3. Đề thiếu
4. \(\lim\limits_{x\rightarrow-2^-}f\left(x\right)=3.\left(-2\right)-5=-11\)
\(\lim\limits_{x\rightarrow-2^+}f\left(x\right)=-2a-1\)
Hàm liên tục tại x=-2 khi:
\(-2a-1=-11\Rightarrow a=-5\)
Đúng 0
Bình luận (0)
Nêu định nghĩa hàm liên tục tại một điểm, trên một khoảng. Nêu nhận xét về đồ thị của một hàm số liên tục trên một khoảng.
+ Hàm số liên tục tại một điểm

+ Hàm số liên tục trên một khoảng
- Hàm số y = f(x) được gọi là liên tục trên một khoảng nếu nó liên tục tại mọi điểm thuộc khoảng đó.
- Hàm số y = f(x) được gọi là liên tục trên một đoạn [a; b] nếu nó liên tục tại mọi điểm thuộc khoảng (a;b) và
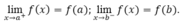
Đồ thị của hàm số liên tục trên một khoảng là một “đường liền” trên khoảng đó.
Đúng 0
Bình luận (0)
Nêu ví dụ về quyền chiếm hữu liên tục
Tham khảo:
Bạn có một chiếc xe máy, đăng ký xe mang tên của bạn chứng tỏ sự chứng nhận của Nhà nước bạn là chủ sở hữu chiếc xe đó. Với chiếc xe bạn có:
– Quyền chiếm hữu: chiếc xe đó là của bạn và không ai được cầm giữ chiếc xe (tức chiếm hữu làm của riêng) mà không được phép của bạn
Đúng 1
Bình luận (0)
Em có một chiếc xe đạp điện , em đã đăng kí giấy chứng nhận xe , được nhà nước công nhận và chiếc xe đạp điện đã thuộc về quyền sở hữu của em.Nếu như em không cho phép ai đụng đến chiếc xe đạp điện thì người đó không có quyền nào được đụng đến vì chưa có sự cho phép của em.
Đúng 1
Bình luận (0)
refer
Ví dụ: sinh viên A đi học, gửi xe của mình cho người trông xe B ở bãi xe nhà trường thì sinh viên A là người chiếm hữu về mặt pháp lý đối với tài sản, B là người chiếm hữu về mặt thực tế đối với tài sản
Đúng 0
Bình luận (0)
Cho hàm số \(y=f\left(x\right)\) liên tục trên đoạn [a; b]. Nếu \(f\left(a\right).f\left(b\right)>0\) thì phương trình \(f\left(x\right)=0\) có nghiệm hay không trong khoảng (a;b) ? Cho ví dụ minh họa ?
Cho hàm số \(y=f\left(x\right)\) liên tục trên đoạn [a; b]. Nếu \(f\left(a\right).f\left(b\right)< 0\) thì phương trình \(f\left(x\right)=0\) có nghiệm hay không trong khoảng (a;b) ? Cho ví dụ minh họa ?
Cho hàm số
f
x
xác định trên
a
;
b
. Có bao nhiêu khẳng định sai trong các khẳng định sau? (I) Nếu
f
x
liên tục trên
a
;
b
và
f
a
.
f
b
0
thì phương trình
f...
Đọc tiếp
Cho hàm số f x xác định trên a ; b . Có bao nhiêu khẳng định sai trong các khẳng định sau?
(I) Nếu f x liên tục trên a ; b và f a . f b < 0 thì phương trình f x = 0 không có nghiệm trên a ; b
(II) Nếu f a . f b < 0 thì hàm số f x liên tục trên a ; b
(III) Nếu f x liên tục trên a ; b và f a . f b < 0 thì phương trình f x = 0 có ít nhất một nghiệm trên a ; b
(IV) Nếu phương trình f x = 0 có nghiệm trên a ; b thì hàm số f x liên tục trên a ; b
A. 1
B. 3
C. 2
D. 4
Đáp án B
Có 1 khẳng định đúng là: Nếu f x liên tục trên a ; b và f a . f b < 0 thì phương trình f x = 0 có ít nhất một nghiệm trên a ; b
Đúng 0
Bình luận (0)
Cho hàm số y f(x) liên tục trên [a;b] Giả sử hàm số u u(x) có đạo hàm liên tục trên [a;b] và
u
(
x
)
∈
[
a
;
b
]
hơn nữa u(x) liên tục trên đoạn [a;b]Mệnh đề nào sau đây là đúng?
Đọc tiếp
Cho hàm số y = f(x) liên tục trên [a;b] Giả sử hàm số u = u(x) có đạo hàm liên tục trên [a;b] và u ( x ) ∈ [ a ; b ] hơn nữa u(x) liên tục trên đoạn [a;b]Mệnh đề nào sau đây là đúng?