a: Thay m=2 vào y=(m-1)x+m-1, ta được:

y=(2-1)x+2-1=x+1

Phương trình hoành độ giao điểm là:

x+1=-x+1

=>2x=0

=>x=0

Thay x=0 vào y=x+1, ta được:

y=0+1=1

Vậy: Tọa độ giao điểm là A(0;1)

b: Thay x=3 và y=4 vào y=(m-1)x+m-1, ta được;

3(m-1)+m-1=4

=>4(m-1)=4

=>m-1=1

=>m=2

c: Để hai đường thẳng này cắt nhau thì \(m-1\ne-1\)

=>\(m\ne0\)

1.

\(a,\Leftrightarrow2m-1+m-2=6\Leftrightarrow3m=9\Leftrightarrow m=3\\ b,2x+3y-5=0\Leftrightarrow3y=-2x+5\Leftrightarrow y=-\dfrac{2}{3}x+\dfrac{5}{3}\)

Để \(\left(d\right)\text{//}y=-\dfrac{2}{3}x+\dfrac{5}{3}\Leftrightarrow\left\{{}\begin{matrix}2m-1=-\dfrac{2}{3}\\m-2\ne\dfrac{5}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=\dfrac{1}{6}\\m\ne\dfrac{11}{3}\end{matrix}\right.\Leftrightarrow m=\dfrac{1}{6}\)

\(c,x+2y+1=0\Leftrightarrow2y=-x-1\Leftrightarrow y=-\dfrac{1}{2}x-\dfrac{1}{2}\\ \left(d\right)\bot y=-\dfrac{1}{2}x-\dfrac{1}{2}\Leftrightarrow\left(-\dfrac{1}{2}\right)\left(2m-1\right)=-1\\ \Leftrightarrow\dfrac{1}{2}\left(2m-1\right)=1\Leftrightarrow m-\dfrac{1}{2}=1\Leftrightarrow m=\dfrac{3}{2}\)

2.

Gọi điểm cố định đó là \(A\left(x_0;y_0\right)\)

\(\Leftrightarrow y_0=\left(2m-1\right)x_0+m-2\\ \Leftrightarrow2mx_0+m-x_0-2-y_0=0\\ \Leftrightarrow m\left(2x_0+1\right)-\left(x_0+y_0+2\right)=0\\ \Leftrightarrow\left\{{}\begin{matrix}2x_0=-1\\x_0+y_0+2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_0=-\dfrac{1}{2}\\y_0=-\dfrac{3}{2}\end{matrix}\right.\)

a: Thay x=1 và y=3 vào d, ta được:

\(m-2+3m+1=3\)

\(\Leftrightarrow4m=4\)

hay m=1

Xét hệ phương trình m − 2 x + m − 6 y = − m + 1 m − 4 x + 2 m − 3 y = m − 5  có định thức cấp hai là

D = m − 2 m − 6 m − 4 2 m − 3 =     m − 2 . 2 m − 3 − m − 4 .   m − 6

= m 2 + 3 m − 18 = m − 3 m + 6

Để hai đường thẳng cắt nhau thì hệ phương trình có nghiệm duy nhất

⟺ D ≠ 0 ⟺ m ≠ 3 m ≠ − 6

ĐÁP ÁN C

Ta có (m – 2)x + (m – 6)y + m – 1 = 0 đúng với mọi m

⇔ mx  - 2x + my -  6y +  m – 1= 0 đúng với mọi m

⇔ (mx + my + m ) + ( -2x – 6y - 1)= 0 đúng với mọi m

⇔ m (x + y + 1) – (2x + 6y + 1) = 0 đúng với mọi m

Điểm cố định của d thỏa mãn

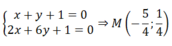
Đáp án D

1: Thay x=-1 và y=1 vào (d), ta được:

-2(a+1)+15-2a=1

=>-2a+2+15-2a=1

=>-4a+17=1

=>-4a=-16

hay a=4

2: Phươg trình hoành độ giao điểm là:

\(x^2-\left(2a+2\right)x-15+2a=0\)

\(\text{Δ}=\left(2a+2\right)^2-4\left(2a-15\right)\)

\(=4a^2+8a+4-8a+60\)

\(=4a^2+64>0\)

Do đó: (P) luôn cắt (d) tại hai điểm phân biệt

2: Theo đề, ta có: \(x_1+x_2+x_1^2+x_2^2=2a+27\)

\(\Leftrightarrow\left(x_1+x_2\right)+\left(x_1+x_2\right)^2-2x_1x_2=2a+27\)

\(\Leftrightarrow2a+27=\left(2a+2\right)+\left(2a+2\right)^2-2\left(2a-15\right)\)

\(\Leftrightarrow4a^2+8a+4+2a+2-4a+30=2a+27\)

\(\Leftrightarrow4a^2+6a+36-2a-27=0\)

\(\Leftrightarrow4a^2+4a+9=0\)

hay \(a\in\varnothing\)

\(a,d//d_1\Leftrightarrow\left\{{}\begin{matrix}m+2=-2\\m\ne3\end{matrix}\right.\Leftrightarrow m=-4\\ b,d\perp d_2\Leftrightarrow\dfrac{1}{3}\left(m+2\right)=-1\Leftrightarrow m+2=-3\Leftrightarrow m=-5\\ c,d.qua.N\left(1;3\right)\Leftrightarrow x=1;y=3\Leftrightarrow3=m+2+m\\ \Leftrightarrow2m=1\Leftrightarrow m=\dfrac{1}{2}\)

\(d,\) Gọi điểm đó là \(A\left(x_1;y_1\right)\)

\(\Leftrightarrow y_1=\left(m+2\right)x_1+m\\ \Leftrightarrow y_1-mx_1-2x_1-m=0\\ \Leftrightarrow-m\left(x_1+1\right)+y_1-2x_1=0\\ \Leftrightarrow\left\{{}\begin{matrix}x_1+1=0\\y_1-2x_1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=-1\\y_1=-2\end{matrix}\right.\)

Vậy \(A\left(-1;-2\right)\) luôn đi qua D với mọi m