Cho tam giác ABC biết \(a=14cm,b=18cm,c=20cm\). Tính \(\widehat{A};\widehat{B};\widehat{C}\) ?

Những câu hỏi liên quan
Cho tam giác ABC có ba cạnh AB = 14cm, AC = 20cm và BC = 18cm. Trên cạnh AB lấy điểm E sao cho AE = 10cm. Trên cạnh AC lấy điểm D sao cho AD = 7cm.
a/ Chứng minh tam giác ADE ~ tam giác ABC
b/ Tính DE
Hình bạn tự vẽ ạ.
a, Xét \(\Delta ADE\) và \(\Delta ABC\) có :
\(\dfrac{AD}{AB}=\dfrac{7}{14}=\dfrac{1}{2}\)
\(\dfrac{AE}{AC}=\dfrac{10}{20}=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{AD}{AB}=\dfrac{AE}{AC}\left(=\dfrac{1}{2}\right)\)
Mà \(\widehat{A}:chung\)
\(\Rightarrow\Delta ADE\sim\Delta ABC\left(c-g-c\right)\)
b, Ta có : \(\Delta ADE\sim\Delta ABC\left(cmt\right)\)
\(\Rightarrow\dfrac{AD}{AB}=\dfrac{ED}{BC}\)
hay \(\dfrac{7}{14}=\dfrac{ED}{18}\)
\(\Rightarrow ED=\dfrac{7.18}{14}=9\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có
a) AB=16cm BC=14cm góc b=60•.Tính các cạnh các góc còn lại và tính diện tích tam giác ABC
b) AB=16cm BC=14cm CA=24cm.Tính các góc và tính diện tích tam giác ABC
c) góc a=50• AB=20cm góc b=60•.Tính các cạnh các góc còn lại và tính diện tích tam giác ABC
Bạn kể thêm đường cao và đặt ẩn là làm ra
Đúng 0
Bình luận (0)
Giải tam giác ABC vuông tại A, biết rằng :
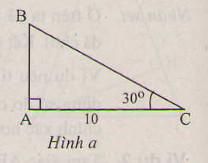
a) \(b=10cm,\widehat{C}=30^0\)
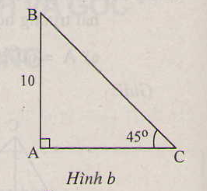
b) \(c=10cm,\widehat{C}=45^0\)
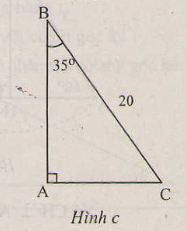
c) \(a=20cm,\widehat{B}=35^0\)
d) \(c=21cm,b=18cm\)
: Cho △ABC; AB = 14cm, AC = 21cm. AD là phân giác của A.Biết BD=8 cm. Độ dài cạnh BC là:
A. 15cm B. 18cm C. 20cm D 22cm
Cho tam giác ABC cân có AB=4cm, AC=8cm.Chu vi của tam giác ABC là:
A.16cm
B.12cm
C.20cm
D.18cm
Do tam giác ABC cân AB =4cm, AC = 8cm => BC = 8cm
Chu vi tam giác sẽ là: 4 +8 +8 = 20cm
Đáp án C
Các bạn muốn giải đáp thắc mắc hoặc kèm thêm toán thì có thể liên hệ nhé
Đúng 2
Bình luận (0)
Do tam giác ABC cân AB =4cm, AC = 8cm => BC = 8cm
Chu vi tam giác sẽ là: 4 +8 +8 = 20cm
Đúng 2
Bình luận (0)
Xem thêm câu trả lời
Tính chu vi của các hình sau :
a) Hình tam giác có độ dài các cạch là 15cm,20cm,25cm
b) Hình tứ giác có độ dài các cạnh là 12cm , 14cm, 16cm , 18cm
a,chu vi của hình tam giác là :
15 + 20 + 25 = 60 ( cm )
đáp số : 60 cm
b, chu vi của hình tứ giác là :
12 + 14 + 16 + 18 = 60 ( cm )
đáp số : 60 cm
Đúng 2
Bình luận (0)
a) Chu vi của tam giác đó là
15+20+25=60 (cm)
Đáp số: 60 cm
b) Chu vi của tứ giác đó là
12+14+16+18=60 (cm)
Đáp số: 60cm
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Giải tam giác ABC vuông tại A, biết rằng
a
)
b
10
cm
,
C
^
30
°
b
)
c
10
c...
Đọc tiếp
Giải tam giác ABC vuông tại A, biết rằng
a ) b = 10 cm , C ^ = 30 ° b ) c = 10 c m , C ^ = 45 ° c ) a = 20 cm , B ^ = 35 ° d ) c = 21 cm , b = 18 cm
(Lưu ý: ΔABC vuông tại A nên ∠ B + ∠ C = 90 °
Giải tam giác tức là đi tìm số đo các cạnh và các góc còn lại.)
a)
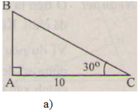
∠ B = 90 o - ∠ C = 90 ° - 30 ° = 60 °
c = b . t g C = 10 . t g 30 ° ≈ 5 , 77 ( c m )
![]()
b)
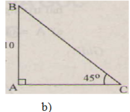
∠ B = 90 ° - ∠ C = 90 ° - 45 ° = 45 °
=> ΔABC cân => b = c = 10 (cm)
![]()
c)
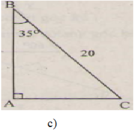
∠ B = 90 o - ∠ C = 90 ° - 35 ° = 55 ° b = a sin B = 20 . sin 35 ° ≈ 11 , 47 ( c m ) c = a sin C = 20 . sin 55 ° ≈ 16 , 38 ( c m )
d)
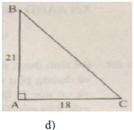
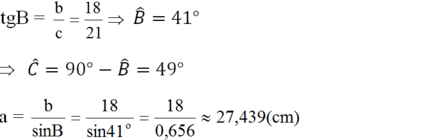
(Ghi chú: Bạn nên sử dụng các kí hiệu cạnh là a, b, c (thay vì BC, AC, AB) để đồng bộ với đề bài đã cho.
Cách để nhớ các cạnh là: cạnh nào thiếu chữ cái nào thì chữ cái đó là kí hiệu của cạnh đó. Ví dụ: cạnh AB thiếu chữ cái C nên c là kí hiệu của cạnh.
hoặc cạnh đối diện với góc nào thì đó chính là kí hiệu của cạnh. Ví dụ: cạnh đối diện với góc B là cạnh b (chính là cạnh AC))
Đúng 0
Bình luận (0)
Tính các góc và các cạnh còn lại của tam giác ABC vuông tại A , biết :
a. AC = 10cm , góc C = 30 độ
b. BC = 20cm , góc B = 40 độ
c. AB = 21cm , AC = 18cm
a) Ta có: ΔABC vuông tại A(gt)
nên \(\widehat{B}+\widehat{C}=90^0\)
hay \(\widehat{B}=60^0\)
Xét ΔABC vuông tại A có
\(AB=AC\cdot\tan30^0\)
\(\Leftrightarrow AB=10\cdot\dfrac{\sqrt{3}}{3}=\dfrac{10\sqrt{3}}{3}\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=10^2+\left(\dfrac{10\sqrt{3}}{3}\right)^2=\dfrac{400}{3}\)
hay \(BC=\dfrac{20\sqrt{3}}{3}\left(cm\right)\)
Đúng 1
Bình luận (0)
Tính các góc và các cạnh còn lại của tam giác ABC vuông tại A , biết :
a. BC = 20cm , góc B = 40 độ
b. AB = 21cm , AC = 18cm
a) Ta có: ΔABC vuông tại A(gt)
nên \(\widehat{B}+\widehat{C}=90^0\)
hay \(\widehat{C}=50^0\)
Xét ΔABC vuông tại A có
\(AB=BC\cdot\sin\widehat{C}\)
\(\Leftrightarrow AB=20\cdot\sin50^0\)
hay \(AB\simeq15,32\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow AC^2=20^2-15.32^2=165.2976\)
hay \(AC\simeq12,86\left(cm\right)\)
Đúng 0
Bình luận (0)