Giả sử rằng \(r=\frac{p}{q}\) là nghiệm hữu tỉ của phương trình, trong đó \(p,q\) là các số nguyên, nguyên tố cùng nhau (tức phân số \(\frac{p}{q}\) tối giản).

Ta có ngay \(ap^2+bpq+q^2c=0\to4a^2p^2+4abpq+4acq^2=0\to\left(2ap+bq\right)^2=\left(bq\right)^2-4acq^2\)

Nếu q là số chẵn thì \(ap^2\) là số chẵn và do đó p chẵn, mâu thuẫn với tính nguyên tố cùng nhau.

Nếu q là số lẻ thì \(bq,2ap+bq\) là các số lẻ. Mặt khác một số chính phương lẻ luôn chia 8 dư 1 nên ta

suy ra \(\left(2ap+bq\right)^2-\left(bq\right)^2\vdots8.\) Do đó \(4acpq\vdots8\to acpq\vdots2\to p\vdots2\). Từ phương trình đầu suy ra \(cq^2\vdots2\to q\vdots2\), vô lí.

Cách khác:

Đặt \(a=2p+1;b=2q+1;c=2r+1\left(p,q,r\in Z\right)\)

Giả sử phương trình \(ax^2+bx+c=0\) không có nghiệm hữu tỉ thì \(\Delta=b^2-4ac\) phải là số chính phương

Ta có:\(\Delta=\left(2q+1\right)^2-4\left(2r+1\right)\left(2p+1\right)\)

\(=4q^2+4q+1-\left(8r-4\right)\left(2p+1\right)\)

\(=4q^2+4q+1-\left(16pr+8r-8p-4\right)\)

\(=4q^2+4q-16pr+8r-8p+5\)

\(=8\left[\frac{q\left(q+1\right)}{2}-2pr+r-p\right]+5\equiv5\left(mod8\right)\)

vô lý vì số chính phương lẻ không thể chia 8 dư 5

=> đpcm

a ơi tại sao b^2-4ac là số chính phương ạ

bạn tham khảo nha

BÀI TOÁN PHỤ: CHứng minh rằng số chính phương lẻ chia cho 8 dư 1.

Giải: Xét số chính phương lẻ là \(m^2\left(m\in Z\right)\)

Như vậy m là số lẻ, đặt \(m=2n+1\)

Ta có:

\(m^2=\left(2n+1\right)^2=4n^2+4n+1=4.n.\left(n+1\right)+1\)

Vì n(n+1) là tích 2 số nguyên liên tiếp nên chia hết cho 2

\(\Rightarrow4n\left(n+1\right) \) chia hết cho 8

\(\Rightarrow4.n.\left(n+1\right)+1\) chia 8 dư 1

Vậy ta có điều phải chứng minh.

Vì a lẻ nên \(a\ne0\), phương trình \(ax^2+bx+c=0\) là phương trình bậc hai.

Xét \(\Delta=b^2-4ac\): b lẻ, theo bài toán phụ có \(b^2=8k+1\left(k\in Z\right)\)

a,c lẻ \(\Rightarrow\) \(ac\) lẻ

Đặt \(ac=2l-1\left(l\in Z\right)\)

Do đó \(\Delta=b^2-4ac=8k+1-4.\left(2l-1\right)=8k+1-8l+4=8\left(k-l\right)+5 \)chia cho 8 dư 5, theo bài toán phụ trên ta có \(\Delta\) không phải số chính phương.

\(\Delta\) là số nguyên, không phải óố chính phương \(\Rightarrow\sqrt{\Delta}\) là số vô tỉ

Nghiệm của phương trình đã cho (nếu có) là: \(x=\frac{-b\pm\sqrt{\Delta}}{2a}\)

b,a\(\in Z\), \(\sqrt{\Delta}\) vô tỉ nên x là vô tỉ.

Vậy phương trình có nghiệm nếu có thì các nghiệm ấy không thể là số hữu tỉ.

 

ơng   là phươngax2+bx+c=0

Bài này có sự liên quan giữa các số lẻ a;b;c không? ( không = khó )

ax^2 +bx +c = 0 (*)
(*) có nghiệm hữa tỷ <=> Δ = b^2 - 4ac là số chính phương lẻ
(vì 4ac chẵn và b lẻ)
Δ là số chính phương lẻ nên Δ chia 8 dư 1 (*)
với a, b , c là số nguyên lẻ nên có dạng:
a = 2m + 1; b = 2n +1; c = 2p + 1 ( m,n,p là số nguyên)
=> Δ = (2n +1)^2 - 4(2m+1)(2p+1)
= 4n^2 + 4n + 1 - 4(4mp + 2m + 2p + 1)
= 4n(n+1) - 8(mp + m + p) - 3 = 4n(n+1) - 8(mp + m + p) - 8 + 5
vì 4n(n+1) - 8(mp + m + p) - 8 chia hết cho 8 => Δ chia 8 dư 5 mâu thuẩn với (*)
=> đpcm.
-------------------------
chứng minh (*):
A = (2k+1)^2 = 4k^2 + 4k + 1 = 4k(k + 1) + 1
k(k + 1) là tích 2 số nguyên liêu tiếp chia hết cho 2
=> 4k(k + 1) chia hết cho 8
=> A chia 8 dư 1

Gọi nghiệm nguyên của P(x) là: k

ta có: \(ak^3+bk^2+ck+d=0\)

\(k.\left(ak^2+bk+k\right)=-d\)( *)

ta có: \(P_{\left(1\right)}=a+b+c+d\)

\(P_{\left(0\right)}=d\)

mà P(1); P(0) là các số lẻ

=> a+b+c+d và d là các số lẻ

mà d là số lẻ

=> a+b+c là số chẵn

Từ (*) => k thuộc Ư(d)

mà d là số lẻ

=> k là số lẻ

=> \(k^3-1;k^2-1;k-1\)là các số chẵn

\(\Rightarrow a\left(k^3-1\right)+b\left(k^2-1\right)+c\left(k-1\right)\) là số chẵn

\(=\left(ak^3+bk^2+ck\right)-\left(a+b+c\right)\)

mà a+b+c là số chẵn

\(\Rightarrow ak^3+bk^2+c\) là số chẵn

Từ (*) => d là số chẵn ( vì d là số lẻ)

=> P(x) không thể có nghiệm nguyên

Chọn B.

Đặt

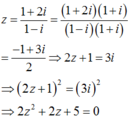
Điều này chứng tỏ z là một nghiệm (phức) của phương trình  2 x 2 + 2 x + 5 = 0

Từ đó suy ra