Viết phương trình đường thẳng \(y=ax+b\) ứng với hình sau :
Những câu hỏi liên quan
Viết phương trình đường thẳng y = ax + b ứng với hình sau
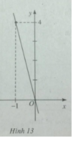
Viết phương trình đường thẳng y = ax + b ứng với hình sau
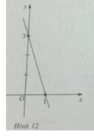
Ta thấy đường thẳng y = ax + b đi qua hai điểm (0; 3) và (1; 0). Vậy ta có:
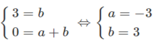
Đường thẳng có phương trình là y = -3x + 3
Đúng 0
Bình luận (0)
Viết phương trình đường thẳng y=ax+b biết đường thẳng đi qua A(-1;2) và vuông góc với đường thẳng x+2y-1=0
\(y=ax+b\left(d\right);y=-\dfrac{1}{2}x+\dfrac{1}{2}\left(d'\right)\)
\(\left(d\right)\perp\left(d'\right)\Leftrightarrow-\dfrac{1}{2}a=-1\Leftrightarrow a=2\Rightarrow y=2x+b\left(d\right)\)
Lại có \(\left(d\right)\) đi qua \(A\left(-1;2\right)\Rightarrow2=-2+b\Rightarrow b=4\)
\(\Rightarrow y=2x+4\left(d\right)\)
Đúng 0
Bình luận (0)
Cho hàm số : y = ax + b
a) Viết phương trình đường thẳng song song Ox ( Dạng đoạn thẳng )
b) Viết phương trình đường thẳng song song Oy
Viết phương trình của đường thẳng y=ax+b song song với đường thẳng y=2x-1
và đi qua một điểm trên trục tung có tung độ là -2.
Viết phương trình y = ax + b của đường thẳng: Đi qua điểm A(1 ; -1) và song song với Ox.
+ Đường thẳng song song với Ox có dạng y = b.
+ Đường thẳng đi qua điểm A(1 ; –1) nên b = – 1.
Vậy đường thẳng cần tìm là y = –1.
Đúng 0
Bình luận (0)
Viết phương trình đường thẳng (d): y-ax+b, biết đường thẳng (d) song song với (d'): y=3x-1 và (d) cắt trục tung tại điểm có tung độ bằng 4.
Vì (d)//(d') nên a=3
Vậy: y=3x+b
Thay x=0 và y=4 vào y=3x+b, ta được:
b=4
Đúng 0
Bình luận (0)
Viết phương trình y = ax + b của đường thẳng: Đi qua hai điểm A(4;3), B(2 ; -1)
+ A (4; 3) thuộc đường thẳng y = ax + b ⇒ 3 = 4.a + b (1)
+ B (2; –1) thuộc đường thẳng y = ax + b ⇒ –1 = 2.a + b (2)
Lấy (1) trừ (2) ta được: 3 – (–1) = (4a + b) – (2a + b)
⇒ 4 = 2a ⇒ a = 2 ⇒ b = –5.
Vậy đường thẳng đi qua hai điểm A(4;3), B(2 ; –1) là y = 2x – 5.
Đúng 0
Bình luận (0)
Viết phương trình của đường thẳng y=ax+b thỏa mãn một trong hai điều kiện sau : Có hệ số góc bằng -2 và đi qua điểm A(-1;2)