Cho hình bình hành ABCD. Chứng minh rằng :
\(\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}=2\overrightarrow{AC}\)
Cho hình bình hành ABCD tâm O.Khẳng định nào sau đây sai?
A, \(\overrightarrow{AB}-\overrightarrow{AD}=\overrightarrow{BD}\)
B. \(\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}\)
C. \(\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AO}\)
D. \(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=\overrightarrow{0}\)
A sai
\(\overrightarrow{AB}-\overrightarrow{AD}=\overrightarrow{AB}+\overrightarrow{DA}=\overrightarrow{DA}+\overrightarrow{AB}=\overrightarrow{DB}=-\overrightarrow{BD}\) mới đúng
Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Chứng minh: \(\overrightarrow{AC}-\overrightarrow{BA}=\overrightarrow{AD}\) ; \(\left|\overrightarrow{AB}+\overrightarrow{AD}\right|=AC\)
a) Chứng minh \(\overrightarrow{AC}-\overrightarrow{BA}=\overrightarrow{AD}\)
Ta có: \(\overrightarrow{AC}-\overrightarrow{CD}=\overrightarrow{AD}\left(đpcm\right)\) ( vì \(\overrightarrow{BA}=\overrightarrow{CD}\) )
b) Chứng minh \(\left|\overrightarrow{AB}+\overrightarrow{AD}\right|=AC\)
Ta có: \(\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}\) ( theo quy tắc hình bình hành )
\(\Rightarrow\left|\overrightarrow{AB}+\overrightarrow{AD}\right|=\left|\overrightarrow{AC}\right|=AC\left(đpcm\right)\)
bài này chả khó áp dụng 1 bước là ra ngay điều cần chứng minh rồi
Cho hình bình hành ABCD , gọi M là trung điểm BC, điểm I thỏa \(\overrightarrow{AI}=\dfrac{2}{3}\overrightarrow{AM}\).Chứng minh rằng \(\overrightarrow{BI}=-\dfrac{2}{3}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\)
a) Cho tứ giác ABCD không phải là hình bình hành, AC cắt BD tại O có OB = OD. Gọi M, N lần lượt là trung điểm của AB và CD, MN cắt AC tại I. Chứng minh rằng \(\overrightarrow{MI}=\overrightarrow{IN}\)
b) Cho tứ giác ABCD có 2 đường chéo cắt nhau tại I. Biết \(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=\overrightarrow{0}\). Chứng minh rằng tứ giác ABCD là hình bình hành
Cho ABCD là hình bình hành (Hình 52). So sánh:
a) Hai vecto \(\overrightarrow {AD} \) và \(\overrightarrow {BC} \).
b) Vecto tổng \(\overrightarrow {AB} + \overrightarrow {AD} \) và vecto \(\overrightarrow {AC} \)
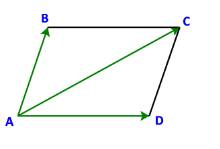
a) Ta có: \(\left\{ \begin{array}{l}AD//BC\\AD = BC\end{array} \right.\) (do tứ giác ABCD là hình bình hành)
\( \Rightarrow \overrightarrow {AD} = \overrightarrow {BC} \)
b) Ta có: \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Cho hình tứ diện ABCD. Chứng minh rằng :
a) \(\overrightarrow{AC}+\overrightarrow{BD}=\overrightarrow{AD}+\overrightarrow{BC}\)
b) \(\overrightarrow{AB}=\dfrac{1}{2}\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{AD}+\dfrac{1}{2}\overrightarrow{CD}+\overrightarrow{DB}\)
Cho hình tứ diện ABCD. Gọi M. N, P, Q lần lượt là trung điểm của các cạnh AC, BD, AD, BC. Chứng minh rằng :
a) \(\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AD}+\overrightarrow{CB}=2\overrightarrow{MN}\)
b) \(\overrightarrow{AB}-\overrightarrow{CD}=\overrightarrow{AC}-\overrightarrow{BD}=2\overrightarrow{PQ}\)
Cho hình bình hành ABCD và điểm E bất kì. Chứng minh: \(\overrightarrow {AB} + \overrightarrow {CE} + \overrightarrow {AD} = \overrightarrow {AE} \).
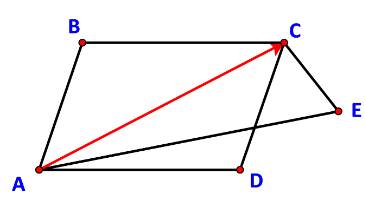
Ta có: \(\overrightarrow {AB} + \overrightarrow {CE} + \overrightarrow {AD} = (\overrightarrow {AB} + \overrightarrow {AD} ) + \overrightarrow {CE} \) (tính chất giao hoán)
Mà theo quy tắc hình bình hành ta có: \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
Suy ra \(\overrightarrow {AB} + \overrightarrow {CE} + \overrightarrow {AD} = \overrightarrow {AC} + \overrightarrow {CE} = \overrightarrow {AE} \)
Vậy \(\overrightarrow {AB} + \overrightarrow {CE} + \overrightarrow {AD} = \overrightarrow {AE} \) với điểm E bất kì.
Cho hình bình hành ABCD. Tìm mối quan hệ giữa hai vectơ \(\overrightarrow {AB} + \overrightarrow {AD} \) và \(\overrightarrow {AC} \)
Vì ABCD là hình bình hành nên \(\left\{ \begin{array}{l}AD//\;BC\\AD = BC\end{array} \right.\), hay \(\overrightarrow {AD} = \overrightarrow {BC} \).
Do đó \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \).