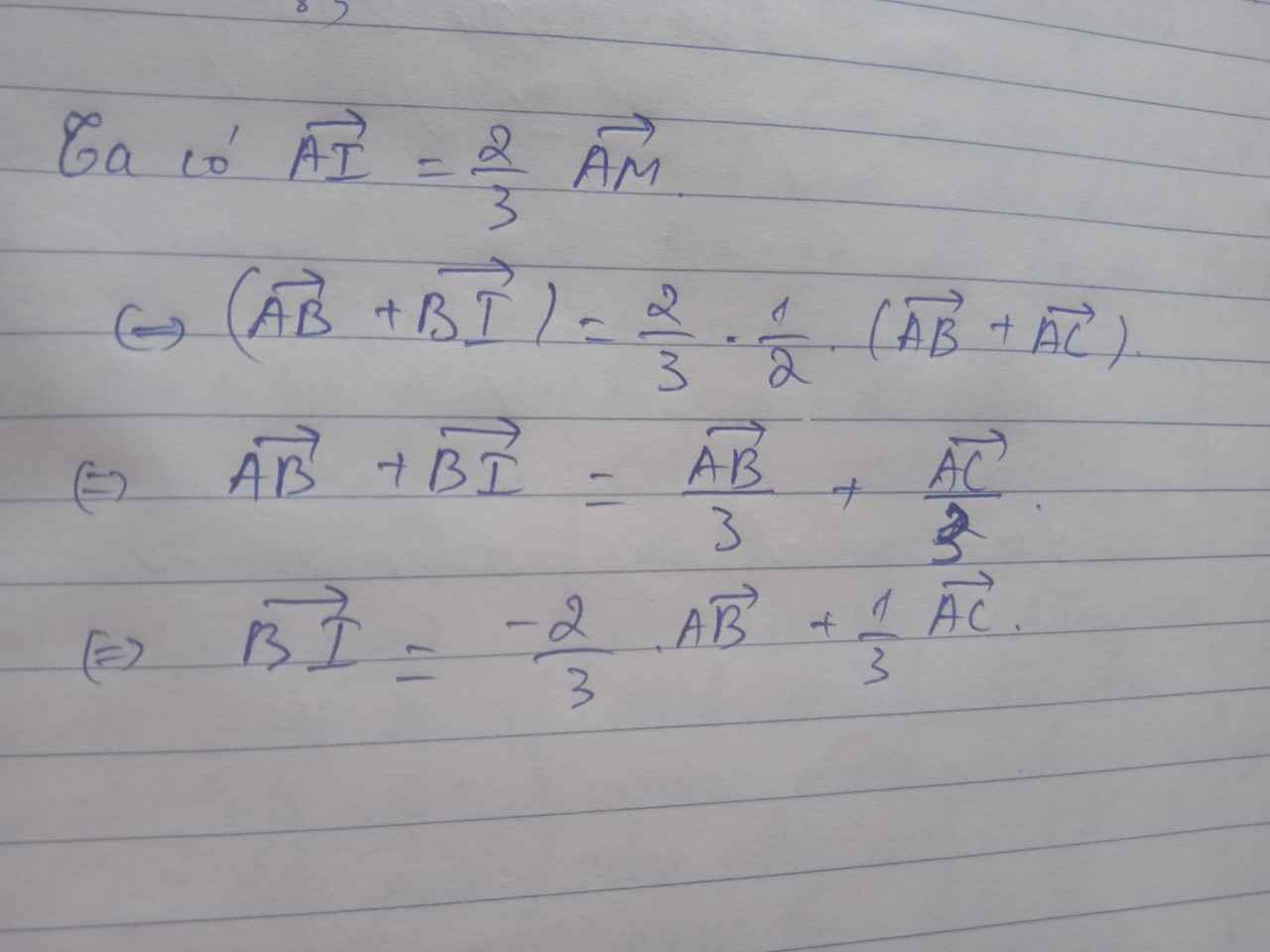§3. Tích của vectơ với một số
Các câu hỏi tương tự
Cho tam giác ABC. Điểm I trên cạnh AC sao cho \(CI=\dfrac{1}{4}CA\). J là điểm mà \(\overrightarrow{BJ}=\dfrac{1}{2}\overrightarrow{AC}-\dfrac{3}{2}\overrightarrow{AB}\)
a) Chứng minh \(\overrightarrow{BI}=\dfrac{3}{4}\overrightarrow{AC}-\overrightarrow{AB}\)
b) Chứng minh B, I, J thẳng hàng
c) Hãy dựng điểm J thỏa mãn điều kiện đề bài
Cho tam giác ABC. Trên hai cạnh AB, AC lấy 2 điểm D và E sao cho overrightarrow{AD}2overrightarrow{DB}, overrightarrow{CE}3overrightarrow{EA}. Gọi M là trung điểm DE và I là trung điểm BC. CMR:
a. overrightarrow{AM}dfrac{1}{3}overrightarrow{AB}+dfrac{1}{8}overrightarrow{AC}
b. overrightarrow{MI}dfrac{1}{6}overrightarrow{AB}+dfrac{3}{8}overrightarrow{AC}
Đọc tiếp
Cho tam giác ABC. Trên hai cạnh AB, AC lấy 2 điểm D và E sao cho \(\overrightarrow{AD}=2\overrightarrow{DB}\), \(\overrightarrow{CE}=3\overrightarrow{EA}\). Gọi M là trung điểm DE và I là trung điểm BC. CMR:
a. \(\overrightarrow{AM}=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{8}\overrightarrow{AC}\)
b. \(\overrightarrow{MI}=\dfrac{1}{6}\overrightarrow{AB}+\dfrac{3}{8}\overrightarrow{AC}\)
cho tam giác ABC, gọi M là điểm trên cạnh BC sao cho\(\overrightarrow{MB}=2\overrightarrow{MC}\) . Chứng minh: \(\overrightarrow{AM}=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AC}\)
cho tam giác ABC có trọng tâm là G và M là trung điểm BC. Khẳng định nào sau đây là saiA. overrightarrow{AG}dfrac{2}{3}overrightarrow{AM} B. overrightarrow{AB}+overrightarrow{AC}3overrightarrow{AG} C. overrightarrow{GA}overrightarrow{BG}+overrightarrow{GC} D.overrightarrow{GB}+overrightarrow{GC}overrightarrow{GM}giúp mk giải câu C , D thôi cx đc tại cô mk bảo phải cm từng câu cho nên m.n giúp mk vs
Đọc tiếp
cho tam giác ABC có trọng tâm là G và M là trung điểm BC. Khẳng định nào sau đây là sai
A. \(\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AM}\)
B. \(\overrightarrow{AB}+\overrightarrow{AC}=3\overrightarrow{AG}\)
C. \(\overrightarrow{GA}=\overrightarrow{BG}+\overrightarrow{GC}\)
D.\(\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{GM}\)
giúp mk giải câu C , D thôi cx đc tại cô mk bảo phải cm từng câu cho nên m.n giúp mk vs
Cho tam giác ABC. Gọi M là trung điểm của BC. Trên cạnh AB,AC lần lượt lấy các điểm P,Q sao cho \(\overrightarrow{AP}=\dfrac{3}{4}\overrightarrow{AB},\overrightarrow{AQ}=\dfrac{2}{3}\overrightarrow{AC}\). Gọi N là giao điểm của AM và PQ. Đặt \(\overrightarrow{NP}=k\overrightarrow{NQ}\).Tìm k
Cho tam giác ABC, G là trọng tâm, I là trung điểm BC, CMR:
a) \(\overrightarrow{AI}=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\)
b) \(\overrightarrow{AG}=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\)
Cho tam giác ABC. Trên các cạnh AB, AC lần lượt lấy các điểm E, F sao cho EB2EA, 2AF3FC. Gọi G là điểm sao cho overrightarrow{BC}2overrightarrow{CG}, M, N lần lượt là trung điểm EF và BC.
a/CMR: overrightarrow{AM}dfrac{1}{6}overrightarrow{AB}+dfrac{3}{10}overrightarrow{AC} và overrightarrow{MN} dfrac{1}{3}overrightarrow{AB}+dfrac{1}{5}overrightarrow{AC}
b/ Phân tích vecto overrightarrow{EG}, overrightarrow{FG} theo 2 vecto overrightarrow{AB}, overrightarrow{AC}
c/Chứng minh rằng 3...
Đọc tiếp
Cho tam giác ABC. Trên các cạnh AB, AC lần lượt lấy các điểm E, F sao cho EB=2EA, 2AF=3FC. Gọi G là điểm sao cho \(\overrightarrow{BC}\)=2\(\overrightarrow{CG}\), M, N lần lượt là trung điểm EF và BC.
a/CMR: \(\overrightarrow{AM}\)=\(\dfrac{1}{6}\)\(\overrightarrow{AB}\)+\(\dfrac{3}{10}\)\(\overrightarrow{AC}\) và \(\overrightarrow{MN}\)= \(\dfrac{1}{3}\)\(\overrightarrow{AB}\)+\(\dfrac{1}{5}\)\(\overrightarrow{AC}\)
b/ Phân tích vecto \(\overrightarrow{EG}\), \(\overrightarrow{FG}\) theo 2 vecto \(\overrightarrow{AB}\), \(\overrightarrow{AC}\)
c/Chứng minh rằng 3 điểm E,F,G thẳng hàng.
Cho hình bình hành ABCD, M là một điểm trên BC sao cho MB = 3MC. Chứng minh \(\overrightarrow{AM}\)= \(\dfrac{1}{4}\overrightarrow{AB}\) + \(\dfrac{3}{4}\overrightarrow{AC}\)
Cho tam giác đều ABC có O là trọng tâm và M là một điểm tùy ý trong tam giác. Gọi D, E, F lần lượt là chân đường vuông góc hạ từ M đền BC, AC, AB. Chứng minh rằng :
\(\overrightarrow{MD}+\overrightarrow{ME}+\overrightarrow{MF}=\dfrac{3}{2}\overrightarrow{MO}\)