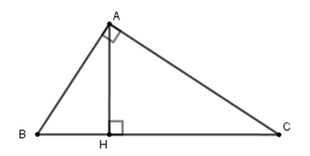
Theo giả thiết AB : AC = 5 : 12

Suy ra A B 5 = A C 12 = A B + A C 5 + 12 = 34 17 = 2 . Do đó AB = 5.2 = 10 (cm);

AC = 2.12 = 24 (cm)

Tam giác ABC vuông tại A, theo định lý Pytago ta có:

B C 2 = A B 2 + A C 2 = 10 2 + 24 2 = 676 , suy ra BC = 26cm

Đáp án cần chọn là: C

Ta có : \(\frac{AB}{AC}\)\(=\frac{5}{12}\Rightarrow AC=\frac{12AB}{5}\left(1\right)\)

Ta có tiếp : \(AC-AB=14Acm\Rightarrow AC=AB+14\left(2\right)\)

Từ ( 1 ) và ( 2 ) => \(\frac{12AB}{5}=AB+14\)

Sau khi tính được \(AB\)thay vào 2 => AC 

Vì ABC vuông nên áp dụng định lý pi-ta-go => BC 

Ta có kết quả AB = 10cm , AC = 24cm ; BC = 26cm

CH/BH=3/4

=>AC/AB=(3/4)^2=9/16

=>AC/9=AB/16=(AC+AB)/(9+16)=14/25=0,56

=>AC=5,04; AB=8,96

BC=căn AC^2+AB^2\(\simeq10,28\)

\(sinC=\dfrac{AB}{BC}\simeq0,87\)

=>góc C=61 độ

=>góc B=29 độ

Bài 1: 

Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:

\(BC^2=AB^2+AC^2\)

\(\Leftrightarrow AC^2=15^2-9^2=144\)

hay AC=12(cm)

Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:

\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=\dfrac{9^2}{15}=\dfrac{81}{15}=5.4\left(cm\right)\\CH=\dfrac{12^2}{15}=\dfrac{144}{15}=9,6\left(cm\right)\end{matrix}\right.\)

Áp dụng định lí Pytago vào ΔAHB vuông tại H, ta được:

\(AH^2+HB^2=AB^2\)

\(\Leftrightarrow AH^2=9^2-5.4^2=51,84\)

hay AH=7,2(cm)

Ta có : \(AB:AC=5:12\)hay \(\frac{AB}{5}=\frac{AC}{12}\Rightarrow\frac{AB^2}{25}=\frac{AC^2}{144}\)

Áp dụng tính chất dãy tỉ số bằng nhau ta có :

\(\frac{AB^2}{25}=\frac{AC^2}{144}=\frac{AB^2+AC^2}{25+144}=\frac{BC^2}{169}=\frac{26^2}{169}=4=2^2\)(vì AB² +AC² = BC²(theo định lí Pitago))

=> \(\orbr{\begin{cases}\frac{AB}{5}=2\\\frac{AC}{12}=2\end{cases}}\Rightarrow\orbr{\begin{cases}AB=10\left(cm\right)\\AC=24\left(cm\right)\end{cases}}\)

bài 2:

ta có: AB<AC<BC(Vì 3cm<4cm<5cm)

=> góc C>góc A> góc B (Các cạnh và góc đồi diện trong tam giác)

Bài 3:

*Xét tam giác ABC, có:

       góc A+góc B+góc c= 180 độ( tổng 3 góc 1 tam giác)

hay góc A+60 độ +40 độ=180độ

  => góc A= 180 độ-60 độ-40 độ.

  => góc A=80 độ

Ta có: góc A>góc B>góc C(vì 80 độ>60 độ>40 độ)

        => BC>AC>AB( Các cạnh và góc đối diện trong tam giác)

bài 2:

ta có: AB <AC <BC (Vì 3cm <4cm <5cm)

=> góc C>góc A> góc B (Các cạnh và góc đồi diện trong tam giác)

Bài 3:

*Xét tam giác ABC, có:

       góc A+góc B+góc c= 180 độ( tổng 3 góc 1 tam giác)

hay góc A+60 độ +40 độ=180độ

  => góc A= 180 độ-60 độ-40 độ.

  => góc A=80 độ

Ta có: góc A>góc B>góc C(vì 80 độ>60 độ>40 độ)

        => BC>AC>AB( Các cạnh và góc đối diện trong tam giác)

HT mik làm giống bạn Dương Mạnh Quyết

ta có: AB<AC<BC(Vì 3cm<4cm<5cm)

=> góc C>góc A> góc B (Các cạnh và góc đồi diện trong tam giác)

Bài 3:

*Xét tam giác ABC, có:

       góc A+góc B+góc c= 180 độ( tổng 3 góc 1 tam giác)

hay góc A+60 độ +40 độ=180độ

  => góc A= 180 độ-60 độ-40 độ.

  => góc A=80 độ

Ta có: góc A>góc B>góc C(vì 80 độ>60 độ>40 độ)

        => BC>AC>AB( Các cạnh và góc đối diện trong tam giác)

C

C

C

Bài 1: (bạn tự vẽ hình vì hình cũng dễ)

Ta có: AB = AH + BH = 1 + 4 = 5 (cm)

Vì tam giác ABC cân tại B => BA = BC => BC = 5 (cm)

Xét tam giác BCH vuông tại H có:

  \(HB^2+CH^2=BC^2\left(pytago\right)\)

  \(4^2+CH^2=5^2\)

  \(16+CH^2=25\)

\(\Rightarrow CH^2=25-16=9\)

\(\Rightarrow CH=\sqrt{9}=3\left(cm\right)\)

Tới đây xét tiếp pytago với tam giác ACH là ra AC nhé

Bài 2: Sử dụng pytago với tam giác ABH => AH

Sử dụng pytago với ACH => AC