Cho tam giác ABC có AB=13cm,AC =12cm,BC=5cm.Chứng minh tam giác ABC là tam giác giác vuông
GIÚP VỚI![]()
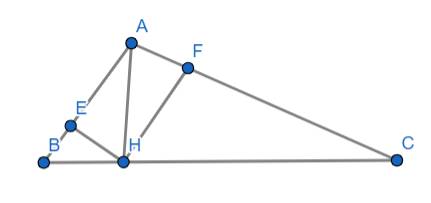
Cho tam giác ABC, AB=5cm,AC=12cm,BC=13cm. AH là đường cao tam giác ABC và AH vuông góc với BC
a, Chứng minh: Tam giác ABC là tam giác vuông và tính AH
b, Kẻ HE vuông góc với AB tại E và HF vuông góc với AC tại F. Chứng minh: AE.AB=AF.AC
c, Tam giác AEF đồng dạng tam giác ABC
d,\(\dfrac{EB}{FC}=(\dfrac{AB}{AC})^{3}\)
e, BC.BE.CF=\(AH^{3}\)
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH=\dfrac{60}{13}\left(cm\right)\)
b: Xét ΔABH vuông tại H có HE là đường cao ứng với cạnh huyền AB
nên \(AE\cdot AB=AH^2\left(1\right)\)
Xét ΔACH vuông tại H có HF là đường cao ứng với cạnh huyền AC
nên \(AF\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)
cho tam giác ABC có BC = 12cm , AC = 5cm , AB = 13cm . Chọn khẳng định đúng
A . tam giác ABC là tam giác vuông tại A
B. tám giác ABC là tam giác nhọn
C. tam giác ABC là tam giác vuông tại C
D . tam giác ABC là tam giác tù
Cho tam giác ABC có ab=5cm,ác=12cm,BC=13cm chứng minh tam giác ABC vuông. Tìm cạnh huyền của tam giác vuông đó
Ta có \(AB^2+AC^2\)=\(5^2+12^2\)=25+144=169
Lại có \(BC^2\)=\(13^2\)=169
\(\Rightarrow AB^2+AC^2=BC^2\)
\(\Rightarrow Tam\) giác ABC vuông tại A
\(\Rightarrow\) Cạnh huyền của tam giác đó là BC
Tam giác ABC cân tại A. Gọi I là trung điểm BC. Vẽ IH vuông góc với AB( H thuộc AB), IK vuông góc với AC(K thuộc AC). Chứng minh rằng:
a) Tam giác ABI = Tam giác ACI
b)Tam giác ΔHBI = Tam giác KCI
c) Cho AC = 13cm, IC = 12cm. Tính AI
Giúp mình với ạ, mình đang cần gấp!
a. Xét 2 tam giác ABI và ACI:
AI chung
AB = AC(tam giác ABC cân tại A)
IB = IC (I là trung điểm của BC)
=> tam giác ABI = tam giác ACI (c-c-c) (đpcm)
=> BI = CI (2 cạnh tương ứng)
b. HI ⊥ AB => H = 90o
KI ⊥ AC => K = 90o
Xét tam giác HBI và tam giác KCI:
H=K=90o
BI = CI(cma)
B = C (tam giác ABC cân tại A)
=> tam giác HBI = tam giác KCI
c. ta có tam giác HBI = tam giác ACI
=> AIB = AIC (2 góc tương ứng)
Mà 2 góc này ở vị trí kề bù.
=> AIB = AIC= \(\dfrac{180^o}{2}\)= 90o
=> tam giác AIC vuông tại I
Áp dụng định lí Py-ta-go vào tam giác AIC, ta có:
AI2 = AC2 - IC2
= 169 - 144 = 36
=> AI = 6 cm
cho tam giác abc có ab =5 cm ac =12cm , bc=13cm
a, tam giác abc có dạng đặc biệt nào? vì sao?
b,vẽ trung tuyến am của tam giác abc . trên tia đối của tia ma lấy điểm k sao cho mk=ma chứng minh tam giác mkc =tam giác mba .từ đó suy ra kc vuông góc với ac
c, tính độ dài am
mọi người giúp mình đc ko ạ mình đang cần rấp gấp
Cho tam giác ABC vuông tại A có AC = 12cm, BC = 13cm. Vẽ tia phân giác BM cửa góc ABC ( M thuộc AC). Từ M kẻ MD vuông góc với BC tại D
a) So sánh các góc của tam giác ABC b) Chứng minh tam giác ABM = tam giác DBM c) Đường thẳng DM cắt tia BA tại K, Chứng minh KD + AB > BCcho tam giác abc có ab=5cm, ac=12cm,bc=13cm
a)chứng minh tam giác ABC vuông tại A và tính độ dài đường cao AH
b)kẻ HE vuong AB tại E , HF vuông AC tại F . Chứng minhAE.AB=AF>AC
c)chứng minh tam giác AFE và tanm giác ABC đồng dạng
cho tam giác abc có AB=5cm AC =12cm BC=13cm
a,cmr tam giác ABC là tam giác vuông
b,gọi h là trung điểm của BC.vẽ he song song với AC(E thuộc AB) vẽ HD vuông góc với AC tại D.cmr tam giác AHE=tam giác HAD
c.cm tam giác BHA cân AHC cân
Cho tam giác ABC cân tại A. Kẻ AM vuông góc với BC (M thuộc BC)
a) Chứng minh tam giác ABM=tam giác ACM
b) Cho biết AB=AC=13cm, AM= 12cm. Tính độ dài cạnh BC
c) Đường thằng vuông góc với AB tại B cắt đường thẳng vuông góc với AC tại C ở D. Chứng minh tam giác DBC cân
Cho tam giác ABC có AB = 5cm AC= 12cm , BC= 13cm C/minh tam giác ABC vuông b) Tính độ dài đường cao AH c) Gọi E, F lần lượt là hình chiếu của H trên AB và AC C/minh góc AFE = góc ABC Mình cần gấp ạ
a) Ta có: \(BC=13cm\Rightarrow BC^2=13^2cm=169cm\)
Xét: \(AB^2+AC^2=5^2+12^2=25+144=169=13^2=BC^2\)
Vậy tam giác ABC vuông tại A có cạnh huyền BC
b) Áp dụng định lý thích hai cạnh góc vuông tà tích giữa cạnh huyền và đường cao ta có:
\(AH\cdot BC=AB\cdot AC\)
\(\Rightarrow AH=\dfrac{AB\cdot AC}{BC}=\dfrac{12\cdot5}{13}\approx4,6\left(cm\right)\)
c) Xét ΔAHB vuông tại H có đường cao HE ta có:
\(\Rightarrow AH^2=AE\cdot AB\) (1)
Xét ΔAHC vuông tại H có đường cao HF ta có:
\(\Rightarrow AH^2=AF\cdot AC\) (2)
Từ (1) và (2)
\(\Rightarrow AB\cdot AE=AC\cdot AF\)
\(\Rightarrow\dfrac{AB}{AF}=\dfrac{AC}{AE}\) (3)
Dựa vào (3)
Ta suy ra: \(\Delta AEF\sim\Delta ABC\)
\(\Rightarrow\widehat{AEF}=\widehat{ABC}\) (đpcm)
a: Xét ΔÂBC có BC^2=AB^2+AC^2
nên ΔABC vuông tại A
b: AH=AB*AC/BC=60/13(cm)
c: ΔAHB vuông tại H có HE là đường cao
nên AE*AB=AH^2
ΔAHC vuông tại H có HF là đường cao
nên AF*AC=AH^2
=>AE*AB=AF*AC
=>AE/AC=AF/AB
=>ΔAEF đồng dạng với ΔACB
=>góc AFE=góc ABC