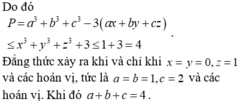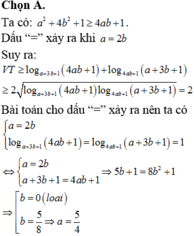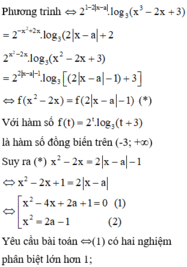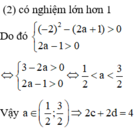Khi đó giá trị của biểu thức
Những câu hỏi liên quan
Cho các số dương a, b, c thỏa mãn
2
a
6
b
12
c
. Khi đó biểu thức
T
b
c
-
b
a
có giá trị là A.
3
2
B. 1 C. 2 D.
1
2
Đọc tiếp
Cho các số dương a, b, c thỏa mãn 2 a = 6 b = 12 c . Khi đó biểu thức T = b c - b a có giá trị là
A. 3 2
B. 1
C. 2
D. 1 2
Chọn đáp án B.
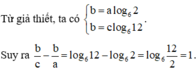
DISCOVERY
Một cách tổng quát chúng ta có các kết quả sau:
1) Cho các số thực dương m, n, p khác 1 và thỏa mãn m.p = n α
Nếu tồn tại các số thực a, b, c thỏa mãn hệ thức 
2) Cho các số thực dương m, n, p khác 1 và thỏa mãn 
Nếu tồn tại các số thực a, b, c thỏa mãn hệ thức 
Đúng 0
Bình luận (0)
Cho a, b, c là các số thực thuộc đoạn [1;2] thỏa mãn . Khi biểu thức đạt giá trị lớn nhất thì giá trị của tổng a+b+c là A. 3 B.
3
.
2
1
3
3
C. 4 D. 6
Đọc tiếp
Cho a, b, c là các số thực thuộc đoạn [1;2] thỏa mãn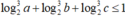 
. Khi biểu thức 
đạt giá trị lớn nhất thì giá trị của tổng a+b+c là
A. 3
B. 3 . 2 1 3 3
C. 4
D. 6
Cho x,y,z là các số thực dương thỏa mãn đẳng thức x^2 + y^2 + z^2 + 2xyz = 1. Khi đó giá trị lớn nhất của biểu thức 2x + y + z bằng bao nhiêu?
C1: Số chữ số của 10^11 là :
C2Tập các giá trị nguyên của x thỏa mãn đẳng thức x=căn bậc 2 của x là S={}.
(Nhập các phần tử theo thứ tự giá trị tăng dần, ngăn cách nhau bởi dấu ‘’;’’)
C3: Cho a;b;c là 3 số khác nhau và khác 0 thỏa mãn: a/b+c=b/a+c=c/a+b . Khi đó giá trị của biểu thức p=b+c/a=a+c/b=a+b/c là p=
1 Cho x,y là các số thỏa mãn I x-3 I + (y+4)^2 = 0
2 Số các giá trị nguyên của x thỏa mãn
2(IxI- 5) ( x^2 -9) =0
3 Nếu 1/2 của a bằng 2b thì 9/8a = kb . Vậy kb =
4 Số giá trị của x thỏa mãn
x^2 +7x +12 = 0
5 Biết (a+1) (b+1) = 551 khi đó giá trị của biểu thức ab+a+b = ?
Cho hai số thực x;y thỏa mãn
x
2
+
y
2
≥
9
và
log
x
2
+
y
2
x
8
x
2
+...
Đọc tiếp
Cho hai số thực x;y thỏa mãn x 2 + y 2 ≥ 9 và log x 2 + y 2 x 8 x 2 + 8 y 2 - 7 x - 7 y 2 ≥ 2 . Gọi giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P=3x+y lần lượt là M và m. Khi đó giá trị của biểu thức M + 2m bằng
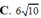
Cho là các số dương thỏa mãn Tìm giá trị nhỏ nhất của biểu thức:
Đọc tiếp
Cho 
Tìm giá trị nhỏ nhất của biểu thức:
biến đổi: \(P=1.\left(\dfrac{1}{16x}+\dfrac{1}{4y}+\dfrac{1}{z}\right)=\left(x+y+z\right)\left(\dfrac{1}{16x}+\dfrac{1}{4y}+\dfrac{1}{z}\right)\)
\(P=\left(\dfrac{y}{16x}+\dfrac{x}{4y}\right)+\left(\dfrac{z}{16x}+\dfrac{x}{z}\right)+\left(\dfrac{z}{4y}+\dfrac{y}{z}\right)+\dfrac{21}{16}\)
Áp dụng bất đẳng thức cosi cho từng ngoặc ta được:
\(\dfrac{y}{16x}+\dfrac{x}{4y}\ge2\sqrt{\dfrac{y}{16x}.\dfrac{x}{4y}}=\dfrac{1}{4}\)
hoàn toàn tương tự: \(\dfrac{z}{16x}+\dfrac{x}{z}\ge\dfrac{1}{2}\)
\(\dfrac{z}{4y}+\dfrac{y}{z}\ge1\)
=> P>=49/16
Đúng 0
Bình luận (0)
Cho hai số thực a và b thỏa mãn
log
a
+
3
b
+
1
a
2
+
4
b
2
+
1
+
log
4
a
b...
Đọc tiếp
Cho hai số thực a và b thỏa mãn log a + 3 b + 1 a 2 + 4 b 2 + 1 + log 4 a b + 1 a + 3 b + 1 = 2 . Khi đó giá trị của biểu thức P=6a+b là
A. 15/8
B. 25/8
C.15/4
D. 25/4
Cho hàm số
f
x
x
6
−
6
x
+
5
x
2
−...
Đọc tiếp
Cho hàm số f x = x 6 − 6 x + 5 x 2 − 2 x + 1 khi x < 1 x 2 + a x + b khi x ≥ 1 , trong đó a, b là các số thực thỏa mãn a 2 + a b + b 2 = 148 . Khi hàm số liên tục trên ℝ , hãy tính giá trị của biểu thức T = a 3 + b 3 .
A. T=2072
B. T=-728
C. T=728
D. T = ± 728
Cho phương trình
4
-
x
-
a
.
log
3
x
2
-
2
x
+
3
+
2
-
x...
Đọc tiếp
Cho phương trình 4 - x - a . log 3 x 2 - 2 x + 3 + 2 - x 2 + 2 x . log 1 3 2 x - a + 2 = 0 . Tập tất cả các giá trị của tham số a để phương trình có 4 nghiệm x 1 ; x 2 ; x 3 ; x 4 thỏa mãn là (c;d). Khi đó giá trị biểu thức T = 2 c + 2 d bằng:
A. 5
B. 2
C. 3
D. 4
