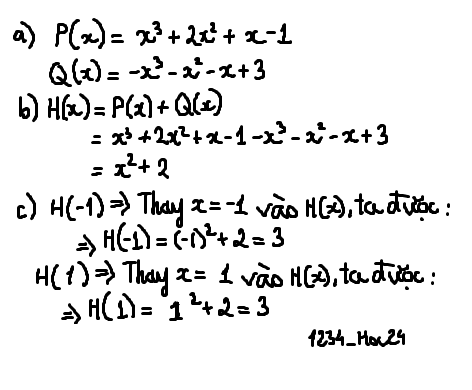1, sắp xếp đa thức
Tìm đa thức
Chứng minh
2, tính độ dài

Những câu hỏi liên quan
cho đa thức A=x^2-3x+x^4-2x+x^2+2
rút gọn đa thức A
sắp xếp A theo lũy thừa tăng
tìm bậc của đa thức
tính giá trị đa thức tại x=1
A = x2 - 3x + x4 - 2x + x2 + 2
A = x4 + ( x2 + x2) - (3x + 2x) + 2
A = x4 + 2x2 - 5x +2
Bậc của đa thức là bậc 4
A(1) = 14 + 2.12 -5.1 + 2
A(1) = 0
Đúng 0
Bình luận (0)
Bài 1: : Cho các đa thức
P(x) = -x3 + 3x2 + x - 1 + 2x3 - x2
Q(x) = -3x3 - x2 + 2x3 + 3x + 3 - 4x
a) Thu gọn và sắp xếp các đa thức trên theo lũy thừa giảm của biến
b) Tìm đa thức H(x) = P(x) + Q(x)
c) Tính H(-1) và H(1)
d) Chứng tỏ rằng đa thức H(x) không có nghiệm.
Cho đa thức
f(x)= 2x^3 - x^5 + 3x^4 + x^2 - 1 phần 2 x^3 + 3 x ^ 5 - 2x^2 - x^4 +1
a) Thu gọn và sắp xếp đa thức trên theo lũy thừa giảm của biến
b) Tìm bậc của đa thức
c) Tính f (1) ; f ( - 1)
a) Ta có:
\(f\left(x\right)=2x^3-x^5+3x^4+x^2-\dfrac{1}{2}x^3+3x^5-2x^2-x^4+1\)
\(f\left(x\right)=\left(-x^5+3x^5\right)+\left(3x^4-x^4\right)+\left(2x^3-\dfrac{1}{2}x^3\right)+\left(x^2-2x^2\right)+1\)
\(f\left(x\right)=2x^5+2x^4+\dfrac{3}{2}x^3-x^2+1\)
Sắp xếp đa thức f(x) the lũy thừa giảm dần của biến, ta được:
\(f\left(x\right)=2x^5+2x^4+\dfrac{3}{2}x^3-x^2+1\)
b) Bậc của đa thức f(x) là 5
c) Ta có:
\(f\left(1\right)=2\cdot1^5+2\cdot1^4+\dfrac{3}{2}\cdot1^3-1^2+1=5,5\) . Vậy f(1) = 5,5.
\(f\left(-1\right)=2\cdot\left(-1\right)^5+2\cdot\left(-1\right)^4+\dfrac{3}{2}\cdot\left(-1\right)^3-\left(-1\right)^2+1=-1,5\). Vậy f(-1) = -1,5.
Đúng 1
Bình luận (0)
1.cho đa thức: Px=x⁴-2x³+x-5+/3x/-2x+2x³ Qx=(2x²-x³)-(2-x⁴-x³)-3x a) Thu gọn đa thức Px,Qx và sắp xếp các hạng tử của mỗi đa thức theo lúy thùa giảm dần của biến. b) tính Ax=Px-Qx c) chứng tỏ x=1 là một nghiệm của đa thức Ax
a) Để thu gọn đa thức Px, ta sắp xếp các hạng tử theo lũy thừa giảm dần của biến x:
Px = x⁴ - 2x³ + x - 5 + / 3x / -2x + 2x³ = x⁴ + 2x³ - 2x³ + x + / 3x / -2x = x⁴ + (2x³ - 2x³) + (x + / 3x / -2x) = x⁴ + (x + / 3x / -2x)
Tương tự, để thu gọn đa thức Qx, ta sắp xếp các hạng tử theo lũy thừa giảm dần của biến x:
Qx = (2x² - x³) - (2 - x⁴ - x³) - 3x = -x³ + 2x² - 2 + x⁴ + x³ - 3x = x⁴ + (-x³ + x³) + 2x² - 3x - 2 = x⁴ + 2x² - 3x - 2
b) Để tính Ax = Px - Qx, ta trừ từng hạng tử của Qx từ Px:
Ax = (x⁴ + (x + / 3x / -2x)) - (x⁴ + 2x² - 3x - 2) = x⁴ + x + / 3x / -2x - x⁴ - 2x² + 3x + 2 = x⁴ - x⁴ + x + / 3x / -2x - 2x² + 3x + 2 = x + / 3x / -2x - 2x² + 3x + 2
c) Để chứng tỏ x = 1 là một nghiệm của đa thức Ax, ta thay x = 1 vào Ax và kiểm tra xem kết quả có bằng 0 hay không:
Ax = 1 + / 3(1) / -2(1) - 2(1)² + 3(1) + 2 = 1 + 3/2 - 2 + 3 + 2 = 6.5
Vì Ax không bằng 0 khi thay x = 1, nên x = 1 không phải là một nghiệm của đa thức Ax.
Đúng 1
Bình luận (0)
a: P(x)=x^4-2x^3+x+2x^3-2x-5+3x
=x^4-x+3x-5
=x^4+2x-5
Q(x)=2x^2-x^3-2+x^4+x^3-3x
=x^4+2x^2-3x-2
b: A(x)=P(x)-Q(x)
=x^4+2x-5-x^4-2x^2+3x+2
=-2x^2+5x-3
c: A(1)=-2+5-3=0
=>x=1 là nghiệm của A(x)
Đúng 0
Bình luận (0)
Cho các đa thức: A(x)=2x\(^3\)+x\(^2\)+1+4x
B(x)= 3x+2+x\(^2\)-2x\(^3\)
a, sắp xếp các đa thức theo lũy thừa giảm dần của biến
b, tính tổng M(x)=A(x)+B(x)
c, tìm nghiệm của đa thức M(x)
a: A(x)=2x^3+x^2+4x+1
B(x)=-2x^3+x^2+3x+2
b: M(x)=A(x)+B(x)
=2x^3+x^2+4x+1-2x^3+x^2+3x+2
=2x^2+7x+3
c: M(x)=0
=>2x^2+7x+3=0
=>2x^2+6x+x+3=0
=>(x+3)(2x+1)=0
=>x=-3 hoặc x=-1/2
Đúng 0
Bình luận (0)
Bài 3 (1,75 điểm): Cho hai đa thức: A(x) 3x6+ 3x3 - 3x3 - 3x6 - x3 + x4 + 2023
B(x) x3 + x2 -1
a. Thu gọn và sắp xếp đa thức A(x) theo luỹ thừa giảm của biến.
b. Tính A(x) + B(x)
c. Biết H(x) – A(x) B(x). Chứng minh đa thức H(x) không có nghiệm
Bài 4 (3điểm): Cho ABC vuông tại A. Tia phân giác của góc ABC cắt AC ở D.Kẻ
DH BC
a. Chứng minh ABD HBD
b. Gọi I là giao điểm của 2 tia BA và HD. Chứng minh IDC cân.
c. Chứng minh: AD +AI 1
2
IC
ét o ét cíu vs mn
Đọc tiếp
Bài 3 (1,75 điểm): Cho hai đa thức: A(x) = 3x6+ 3x3 - 3x3 - 3x6 - x3 + x4 + 2023 B(x) = x3 + x2 -1 a. Thu gọn và sắp xếp đa thức A(x) theo luỹ thừa giảm của biến. b. Tính A(x) + B(x) c. Biết H(x) – A(x) = B(x). Chứng minh đa thức H(x) không có nghiệm Bài 4 (3điểm): Cho ABC vuông tại A. Tia phân giác của góc ABC cắt AC ở D.Kẻ DH BC a. Chứng minh ABD = HBD b. Gọi I là giao điểm của 2 tia BA và HD. Chứng minh IDC cân. c. Chứng minh: AD +AI > 1 2 IC
ét o ét cíu vs mn
Xem thêm câu trả lời
Bài tập 2: Cho hai đa thức:
P(x) = 5x³ - 7x² + 2x* - 5x³ + 2
Q(x) = 2x - 4x² - 2x³ + 5 + 1/2x
a) Sắp xếp các đa thức trên theo luỹ thừa tăng của biến.
b) Tính P(x) + Q(x); P(x) - Q(x).
c) Tìm bậc của đa thức tổng, đa thức hiệu.
cho 2 đa thức sau:
P(x)=2x3-x4+1+2x2+5x4-x3;
Q(x)=-3x4-1+5x3-x2-6x2-4x3
a) Thu gọn và sắp xếp các đa thức trên theo lũy thừa giảm của biến?
b) Tính P(-2)?
c) Tính P(x)+Q(x)?
d) Chứng minh rằng với mọi giá trị của x thì Q(x)-P(x) luôn nhận giá trị âm.
cho 2 đa thức sau:
P(x)=2x3-x4+1+2x2+5x4-x3;
Q(x)=-3x4-1+5x3-x2-6x2-4x3
a) Thu gọn và sắp xếp các đa thức trên theo lũy thừa giảm của biến?
b) Tính P(-2)?
c) Tính P(x)+Q(x)?
d) Chứng minh rằng với mọi giá trị của x thì Q(x)-P(x) luôn nhận giá trị âm.