(h.141)\(\Delta AOM\) cân \(\Rightarrow\)\(\widehat{A}=\widehat{M1}\)

\(\Delta BOM\) cân \(\Rightarrow\)\(\widehat{B}=\widehat{M2}\)

Suy ra \(\widehat{M1}+\widehat{M2}=\widehat{A}+\widehat{B}\)do đó

\(\widehat{AMB}=\widehat{A}+\widehat{B}\).Ta lại có:

\(\widehat{AMB}+\widehat{A}+\widehat{B}=180^0\) nên

\(\widehat{AMB}=90^0\)

(h.141)

cân

Suy ra do đó

.Ta lại có:

nên

ddddddddddddddddddddd

sorry thằng em nó lam nhé 

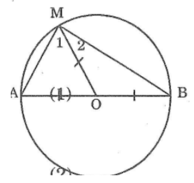
Nối OM, ta có:

OA = OM (bán kính đường tròn tâm O)

Nên ΔOAM cân tại O

⇒∠A =∠M1(tính chất tam giác cân)(1)

OM = OB (bán kính đường tròn tâm O)

Suy ra: ΔOBM cân tại O

⇒∠B =∠M2(tính chất tam giác cân) (2)

Trong ΔAMB ta có:

∠A + ∠AMB + ∠B = 180º (tổng ba góc trong tam giác)

⇒∠A +∠B +∠M1+∠M2 =180 (3)

Từ (1), (2) và (3) suy ra: 2(∠M1 + ∠M2)=180o

Vậy: ∠M1+∠M2=90o hay ∠(AMB) =90o

bạn tự vẽ hình giúp mik nha

a) áp dụng t/c 2 tiếp tuyến cắt nhau ta có

OM là tia phân giác \(\widehat{AOI}\)

ON là tpg \(\widehat{IOB}\)

mà:\(\widehat{AOI}+\widehat{BOI}=180^o\)\(\Rightarrow OM\perp ON\)(t/c 2 góc kề bù)

vậy \(\widehat{MON}=90^o\)

b)từ t/c 2 tiếp tuyến cắt nhau ta có

MA=MI;BN=NI

\(\Rightarrow\)AM+BN=MI+NI=MN9(đpcm)

c)ta có:AM.BN=MI.NI(1)

xét \(\Delta MON\) vuông tại O có

MI.NI(đlý)=\(OI^2=R^2\)(2)

từ (1) và (2)\(\Rightarrow AM.BN=R^2\)

a: Xét (O) có 

ME là tiếp tuyến

MA là tiếp tuyến

Do đó: ME=MA và OM là tia phân giác của góc AOE(1)

Xét (O) có

NE là tiếp tuyến

NB là tiếp tuyến

Do đó: NE=NB và ON là tia phân giác của góc BOE(2)

Từ (1) và (2) suy ra \(\widehat{MON}=\dfrac{1}{2}\cdot\left(\widehat{EOA}+\widehat{EOB}\right)=\dfrac{1}{2}\cdot180^0=90^0\)

b: Ta có: MN=ME+NE

nên MN=MA+NB

c: Xét ΔOMN vuông tại O có OE là đường cao

nên \(OE^2=EM\cdot EN\)

hay \(AM\cdot BN=R^2\)

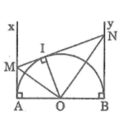
Gọi I là tiếp điểm của tiếp tuyến MN với đường tròn (O). Nối OI

Ta có:  (hai góc kề bù)

OM là tia phân giác của góc AOI (tính chất hai tiếp tuyến cắt nhau)

ON là tia phân giác của góc BOI (tính chất hai tiếp tuyến cắt nhau)

Suy ra : OM ⊥ ON (tính chất hai góc kề bù)

Vậy