Trong mặt phẳng với hệ tọa độ (Oxy),cho hình bình hành ABCD có hai đỉnh A(-2;-1), D(5;0) và có tâm I(2;1).Hãy xác định toạ độ hai đỉnh B,C và góc nhọn hợp bởi hai đường chéo của hình bình hành đã cho.
1.Trong mặt phẳng tọa độ Oxy cho hình bình hành ABCD với A (- 6;1); B (2;2) C (1;5) tọa độ đỉnh D là:
A. (5;2)
B. (-7;4)
C. (5;4)
D. (7;-4)
2.Trong mặt phẳng tọa độ Oxy cho tam giác ABC với A (- 1;3); B (2;1) C (5;5) tọa độ đỉnh D là của hình bình hành ABCD:
A. (0;4)
B. (8;1)
C. (8;3)
D. (-8;3)
Hướng dẫn em cách làm với ạ. Em cảm ơn nhiều.
1, Gọi tọa độ điểm D(x;y)
Ta có:\(\overrightarrow{AB}\left(8;1\right)\)
\(\overrightarrow{DC}\left(1-x;5-y\right)\)
Tứ giác ABCD là hình bình hành khi
\(\overrightarrow{AB}=\overrightarrow{DC}\)
\(\Leftrightarrow1-x=8;5-y=1\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-7\\y=4\end{matrix}\right.\)
Vậy tọa độ điểm D(-7;4)
Trong mặt phẳng tọa độ Oxy cho hình bình hành ABCD có \(A\left(1;-2\right);B\left(3;2\right);C\left(-4;1\right)\). Tìm tọa độ đỉnh D ?
Gọi điểm D(x,y) là điểm cần tìm.
Tứ giác ABCD là hình bình hành khi và chỉ khi: \(\overrightarrow{AB}=\overrightarrow{DC}\).
\(\overrightarrow{AB}\left(2;4\right)\); \(\overrightarrow{DC}\left(-4-x;1-y\right)\).
\(\overrightarrow{AB}=\overrightarrow{DC}\)\(\Leftrightarrow\left\{{}\begin{matrix}-4-x=2\\1-y=4\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=-6\\y=-3\end{matrix}\right.\)\(\Leftrightarrow D\left(-6;-3\right)\).
trong mặt phẳng với hệ tọa độ Oxy, cho hình chữ nhật ABCD có đỉnh A(-1,2) và tâm I(1/2:0) xác định tọa độ các đỉnh còn lại của hình chữ nhật ABCD, biết đường thẳng BC đi qua điểm m(4;-3)
I là trung điểm AC \(\Rightarrow C\left(2;-2\right)\)
\(\Rightarrow\overrightarrow{CM}=\left(2;-1\right)\Rightarrow\) đường thẳng BC có dạng:
\(1\left(x-2\right)+2\left(y+2\right)=0\Leftrightarrow x+2y+2=0\)
Đường thẳng AB qua A và vuông góc BC nên nhận \(\left(2;-1\right)\) là 1 vtpt
Phương trình AB:
\(2\left(x+1\right)-1\left(y-2\right)=0\Leftrightarrow2x-y+4=0\)
B là giao điểm AB và BC nên tọa độ là nghiệm:
\(\left\{{}\begin{matrix}x+2y+2=0\\2x-y+4=0\end{matrix}\right.\) \(\Rightarrow B\left(...\right)\)
I là trung điểm BD \(\Rightarrow\left\{{}\begin{matrix}x_D=2x_I-x_B=...\\y_D=2y_I-y_B=...\end{matrix}\right.\)
Trong mặt phẳng Oxy cho hình bình hành ABCD với A(2;4), B(-3;1), C(3;-1) và D(8;2).
a/ Tính tọa độ chân A' của đường cao vẽ từ đỉnh A của tam giác ABC
b/ Tính diện tích của hình bình hành ABCD
vì trên diễn đàn này toàn câu hỏi hồi rác
ok bạn thực ra mình cũng chang cần k đâu.
nhung mat cong tra loi cho mot nguoi hoi linh tinh that chan
trong mặt phẳng với hệ tọa độ Oxy, cho hình thang cân ABCD ( AB//CD) . biết tọa độ các điểm A(-8;2) B(-4;6)D(-6-8) xác định tọa độ đỉnh C
\(\overrightarrow{AB}=\left(-4;4\right)=-4\left(1;-1\right)\)
\(\Rightarrow\) Phương trình CD song song AB đi qua D có dạng:
\(1\left(x+6\right)+1\left(y+8\right)=0\Leftrightarrow x+y+14=0\)
Gọi M là trung điểm AB \(\Rightarrow M\left(-6;4\right)\)
Phương trình đường thẳng d qua M và vuông góc AB có dạng:
\(1\left(x+6\right)-1\left(y-4\right)=0\Leftrightarrow x-y+10=0\)
Gọi N là giao điểm CD và d \(\Rightarrow\) N là trung điểm CD do ABCD là hình thang cân
Tọa độ N là nghiệm: \(\left\{{}\begin{matrix}x+y+14=0\\x-y+10=0\end{matrix}\right.\) \(\Rightarrow N\left(-12;-2\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x_C=2x_N-x_D=...\\y_C=2y_N-y_D=...\end{matrix}\right.\)
Trong mặt phẳng tọa độ Oxy, cho hình bình hành ABCD biết A(-2; 0); B(2; 5); C( 6; 2).Tìm tọa độ điểm D?
A. D(2; -3)
B. D(2; 3)
C. D(-2; -3)
D. D(-2; 3)
Gọi D(x; y)
Ta có A D → = x + 2 ; y và B C → = 4 ; − 3 .
Vì ABCD là hình bình hành nên A D → = B C →
x + 2 = 4 y = − 3 ⇔ x = 2 y = − 3 ⇒ D 2 ; − 3 .
Chọn A.
Trong mặt phẳng với hệ tọa độ Oxy cho hình bình hành OABC có tọa độ điểm A(3;1), C(-1;2) (tham khảo hình vẽ bên). Số phức nào sau đây có điểm biểu diễn là điểm B?
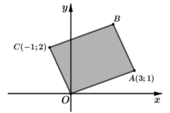
A. z 1 = - 2 + 3 i
B. z 2 = 2 + 3 i
C. z 3 = 4 - i
D. z 4 = - 4 + i
Vì OABC là hình bình hành nên

Suy ra số phức z 2 = 2 + 3 i có điểm biểu diễn là B.
Chọn B.
Trong mặt phẳng với hệ trục tọa độ Oxy cho hình bình hành ABCD có góc ABC nhọn, đỉnh A(-2;-1). Gọi H, K, E lần lượt là hình chiếu vuông góc của A trên các đường thẳng BC, BD, CD. Phương trình đường tròn ngoại tiếp HKE là (C) : \(x^2+y^2+x+4y+3=0\). Tìm tọa độ các đỉnh B, C, D biết H có hoành độ âm, C có hoành độ dương và nằm trên đường thẳng \(x-y-3=0\)
Ta có \(\widehat{AHC}=\widehat{AEC}=90^0\) nên 4 điểm A, H, C, E cùng thuộc đường tròn đường kính AC.
Gọi I là giao điểm của AC và BD
Ta có \(\widehat{HIE}=2\widehat{HAE}=2\left(180^0-\widehat{BCD}\right)\)
Các tứ giác AKED, AKHB nội tiếp nên \(\widehat{EKD}=\widehat{EAD}\) và \(\widehat{BKH}=\widehat{BAH}\)
Do đó \(\widehat{HKE}=180^0-\widehat{AKD}-\overrightarrow{BKH}=180^0-\overrightarrow{EAD}-\overrightarrow{BAH}=2\overrightarrow{HAE}=2\left(180^0-\overrightarrow{BCD}\right)=\overrightarrow{HIE}\)
Vậy tứ giác HKIE nội tiếp. Do đó I thuộc đường tròn (C) ngoại tiếp tam giác HKE
- Gọi \(C\left(c;c-3\right)\in d\left(c>0\right)\Rightarrow I\left(\frac{c-2}{2};\frac{c-4}{2}\right)\)
Do I thuộc (C) nên có phương trình :
\(c^2-c-2=0\Leftrightarrow c=2\) V c=-1 (loại c=-1) Suy ra \(C\left(2;-1\right);I\left(0;-1\right)\)
- Điểm E, H nằm trên đường tròn đường kính AC và đường tròn (C) nên tọa độ thỏa mãn hệ phương trình :
\(\begin{cases}x^2+y^2+x+4y+3=0\\x^2+\left(y+1\right)^2=4\end{cases}\) \(\Leftrightarrow\begin{cases}x=0;y=-3\\x=-\frac{8}{5};y=-\frac{11}{2}\end{cases}\)
- Vì H có hoành độ âm nên \(H\left(-\frac{8}{5};-\frac{11}{5}\right);E\left(0;-3\right)\) Suy ra \(AB:x-y+1=0;BC:x-3y-5=0\)
Tọa độ B thỏa mãn \(\begin{cases}x-y+1=0\\x-3y-5=0\end{cases}\) \(\Leftrightarrow B\left(-4;-3\right)\Rightarrow\overrightarrow{BA}=\left(2;2\right);\overrightarrow{BC}=\left(6;2\right)\Rightarrow\overrightarrow{BA}.\overrightarrow{BC}=16>0\)
Vì \(\overrightarrow{AB}=\overrightarrow{DC}\Rightarrow D\left(4;1\right)\)
Vậy \(B\left(-4;-3\right);C\left(2;-1\right);D\left(4;1\right)\)
Trong mặt phẳng tọa độ Oxy , cho tam giác ABC có A (3;2) , B(-4;2) ,C (3;5) tìm tọa độ điểm D sao cho tứ giác ABCD là hình bình hành
vecto AB=(-7;0)
vecto DC=(3-x;5-y)
Vì ABCD là hình bình hành
nên vecto AB=vecto DC
=>3-x=-7; 5-y=0
=>x=10; y=5
Trong mặt phẳng tọa độ Oxy cho A(3; -1) ; B( -1; 2) và I( 1; -1) . Xác định tọa độ các điểm C; D sao cho tứ giác ABCD là hình bình hành biết I là trọng tâm tam giác ABC. Tìm tọa tâm O của hình bình hành ABCD
A. 
B. 
C. 
D. 