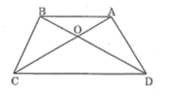
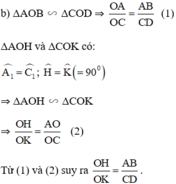Cho hình thang ABCD (AB // CD), có 2 đường chéo AC và BD cắt tại O. Chứng minh rằng OA.OD = OB.OC

Những câu hỏi liên quan
Cho hình thang ABCD (AB // CD), có 2 đường chéo AC và BD cắt tại O. Chứng minh rằng OA.OD = OB.OC
Hình thang ABCD (AB // CD) có hai đường chéo AC và BD cắt nhau tại O
Chứng minh rằng: OA.OD = OB.OC
Ta có: AB // CD (gt), áp dụng hệ quả của định lý Ta – lét ta có:
Suy ra ![]() (hệ quả định lí ta-lét)
(hệ quả định lí ta-lét)
Vậy OA.OD = OB.OC
Đúng 1
Bình luận (0)
Cho hình thang \(ABCD\left( {AB//CD} \right)\) có hai đường chéo \(AC\) và \(BD\) cắt nhau tại \(O\). Chứng minh rằng \(OA.OD = OB.OC\)
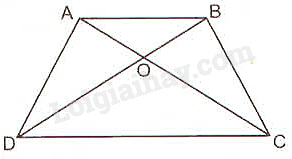
Xét tam giác \(OCD\) có \(AB//CD\) (giả thiết) và \(AB\) cắt \(OC;OD\) lần lượt tại \(A;B\).
Theo hệ quả của định lí Thales ta có:
\(\frac{{OA}}{{OC}} = \frac{{OB}}{{OD}} = \frac{{AB}}{{CD}} \Rightarrow \frac{{OA}}{{OC}} = \frac{{OB}}{{OD}} \Rightarrow OA.OD = OB.OC\) (điều phải chứng minh).
Đúng 0
Bình luận (0)
Cho hình thang \(ABCD\left( {AB//CD} \right)\) có hai đường chéo \(AC\) và \(BD\) cắt nhau tại \(O\). Chứng minh rằng \(OA.OD = OB.OC\)

Xét tam giác \(OCD\) có \(AB//CD\) (giả thiết) và \(AB\) cắt \(OC;OD\) lần lượt tại \(A;B\).
Theo hệ quả của định lí Thales ta có:
\(\frac{{OA}}{{OC}} = \frac{{OB}}{{OD}} = \frac{{AB}}{{CD}} \Rightarrow \frac{{OA}}{{OC}} = \frac{{OB}}{{OD}} \Rightarrow OA.OD = OB.OC\) (điều phải chứng minh).
Đúng 0
Bình luận (0)
cho hình thang ABCD(AB//CD) có 2 đường chéo AC, BD cắt nhau tại O. Chứng minh: OA.OD=OB.OC
Help me !!!
Hình Thang ABCD(AB//CD) có hai đường chéo AC và BD cắt nhau tại O.
Chứng minh rằng: OA.OD=OB.OC
Giúp em lần nữa đi cả nhà
Ta có: \(AB//CD\left(Gt\right)\)
Áp dụng định lí ta - let trong hình thang \(ABCD\)ta có:
\(\Rightarrow\frac{OA}{OC}=\frac{OB}{OD}\Rightarrow OA.OD=OB.OC\left(đpcm\right)\)
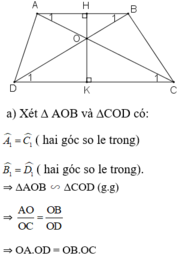
Cho hình thang ABCD (AB // CD). Gọi O là giao điểm của hai đường chéo AC và BD. a) Chứng minh rằng OA.OD OB.OC b) Đường thẳng qua O vuông góc với AB và CD theo thứ tự tại H và K. Chứng minh rằng
O
H
O
K
A
B
C
D
Đọc tiếp
Cho hình thang ABCD (AB // CD). Gọi O là giao điểm của hai đường chéo AC và BD.
a) Chứng minh rằng OA.OD = OB.OC
b) Đường thẳng qua O vuông góc với AB và CD theo thứ tự tại H và K.
Chứng minh rằng O H O K = A B C D
Cho hình thang ABCD có hai đáy là AB và CD, các đường chéo cắt nhau tại O. Chứng minh O A . O D = O B . O C .
Vì AB//CD, áp dụng định lý Ta-lét, ta có: O A O C = O B O D
Từ đó suy ra ĐPCM
Đúng 0
Bình luận (0)
Cho hình thang ABCD có hai đáy là AB và CD, các đường chéo cắt nhau tại O. Chứng minh: OA.OD = OB.OC
Xét tam giác OAB và tam giác OCD ta có :
^AOB = ^COD ( đối đỉnh )
^OAB = ^OCD ( so le trong )
Vậy tam giác OAB ~ tam giác OCD ( g.g )
=> OA/OC = OB/OD => OA.OD = OC.OB
Đúng 3
Bình luận (0)
Vì AB//CD nên:
\(\dfrac{OA}{OC}=\dfrac{OB}{OD}\) ( hệ quả đl ta-lét)
từ đó suy ra : OA.OD=OB.OC(đpcm)
Đúng 3
Bình luận (0)
Cho hình thang ABCD (AB//CD).gọi O là giao điểm 2 đường chéo.
a. Chứng minh rằng : OA.OD=OB.OC
b.Kẻ đường thẳng qua O và song song với CD cắt AD,BC lần lượt tại M và N.Chứng minh rằng: ON=OM.
Xem chi tiết