Vì AB//CD, áp dụng định lý Ta-lét, ta có: O A O C = O B O D
Từ đó suy ra ĐPCM
Vì AB//CD, áp dụng định lý Ta-lét, ta có: O A O C = O B O D
Từ đó suy ra ĐPCM
Cho hình thang ABCD (AB // CD). Hai đường chéo AC và BD cắt nhau tại O. Đường thẳng a qua O và song song với đáy của hình thang cắt các cạnh AD, BC theo thứ tự tại E và F (h.26).
Chứng minh rằng OE = OF
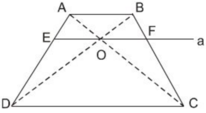
Hình thang ABCD (AB // CD) có hai đường chéo AC và BD cắt nhau tại O. Đường thẳng qua O song song với đáy AB cắt các cạnh bên AD, BC theo thứ tự tại M, N. Chứng minh rằng OM = ON.
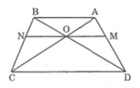
Cho hình thang ABCD (AB //CD). Hai đường chéo AC và BD cắt nhau tại O. Đường thẳng A qua O và song song với đáy của hình thang cắt các cạnh AD, BC theo thứ tự E và F
Chứng minh rằng OE = OF.
Bài 2: a, Cho hình thang ABCD (AB // CD). Một đường thẳng song song với hai đáy, cắt các cạnh bên AD và BC tại E, F. Tính FC biết AE = 4cm; ED = 2cm; BF = 6cm.
b, Cho hình thang ABCD (AB // CD), các đường chéo cắt nhau tại O.
Chứng minh rằng: OA.OD = OB. OC
giúp mik zới các pạn ơi, nhanh nha
Hình thang ABCD ( AB // CD) có hai đường chéo cắt nhau tại O. Đường thẳng qua o và song song với đáy AB cắt các cạnh bên AD, BC theo thứ tự tại M và N.
a. Chứng minh rằng OM = ON.
Cho hình thang ABCD ( AB//CD ) có O là giao điểm của hai đường chéo. Đường thẳng qua O song song hai đáy và cắt AD, BC lần lượt tại E và F. Chứng minh OE = OF.
Cho hình thang ABCD ( AB//CD ) có O là giao điểm của hai đường chéo. Đường thẳng qua O song song hai đáy và cắt AD, BC lần lượt tại E và F. Chứng minh OE = OF.
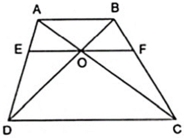
Hình thang ABCD (AB // CD) có hai đường chéo AC và BD cắt nhau tại O. Gọi M, K, N, H lần lượt là chân đường vuông góc hạ từ O xuống các cạnh AB, BC, CD, DA. Chứng minh rằng: O M O N = A B C D
Cho hình thang ABCD (AB // CD) có hai đường chéo cắt nhau tại O. Đường thẳng qua O song song với hai đáy cắt hai cạnh bên tại E và F.
a, Tìm độ dài các cạnh đáy của hình thang biết OC : OA = 1 : 3 và độ dài của đường trung bình là 24cm.
b, C/minh: OE = OF
c, C/minh hệ thức : \(\dfrac{1}{AB}+\dfrac{1}{CD}=\dfrac{2}{EF}\)