Trong ΔDAB, ta có: OM // AB (gt)
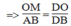 (Hệ quả định lí Ta-lét) (1)
(Hệ quả định lí Ta-lét) (1)
Trong ΔCAB, ta có: ON // AB (gt)
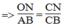 (Hệ quả định lí Ta-lét) (2)
(Hệ quả định lí Ta-lét) (2)
Trong ΔBCD, ta có: ON // CD (gt)
Suy ra: ![]() (định lí Ta-lét) (3)
(định lí Ta-lét) (3)
Từ (1), (2) và (3) suy ra: 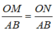
Vậy: OM = ON
Trong ΔDAB, ta có: OM // AB (gt)
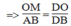 (Hệ quả định lí Ta-lét) (1)
(Hệ quả định lí Ta-lét) (1)
Trong ΔCAB, ta có: ON // AB (gt)
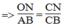 (Hệ quả định lí Ta-lét) (2)
(Hệ quả định lí Ta-lét) (2)
Trong ΔBCD, ta có: ON // CD (gt)
Suy ra: ![]() (định lí Ta-lét) (3)
(định lí Ta-lét) (3)
Từ (1), (2) và (3) suy ra: 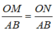
Vậy: OM = ON
Hình thang ABCD ( AB // CD) có hai đường chéo cắt nhau tại O. Đường thẳng qua o và song song với đáy AB cắt các cạnh bên AD, BC theo thứ tự tại M và N.
a. Chứng minh rằng OM = ON.
.Hình thang ABCD (AB//CD) có hai đường chéo cắt nhau tại O. Đường thẳng qua O và song song với đáy AB cắt các cạnh bên AD, BC theo thứ tự lần lượt là ở E và ở F. Chứng minh rằng OM = ON theo cách tính diện tích
Cho hình thang ABCD (AB // CD), có 2 đường chéo AC và BD cắt tại O. Đường thẳng qua O và song song với đáy AB cắt các cạnh bên AD và BC theo thứ tự tại M và N. C/m
a) OA.OD=OB.OC
b)OM=ON
Bài 1: Cho hình thang ABCD ( AB // CD), đường chéo AC và BD cắt nhau tại O. Đường thẳng qua O và song song với AB cắt các cạnh bên AD, BC lần lượt tại M, N.
1. Chứng minh: OM = ON 2. Chứng minh: (AM/AD)+(CN/CB)=1
Cho hình thang ABCD ( AB // CD), đường chéo AC và BD cắt nhau tại O. Đường thẳng qua O và song song với AB cắt các cạnh bên AD, BC lần lượt tại M, N. 1. Chứng minh: OM = ON 2. Chứng minh: (AM/AD)+(CN/CB)=1
Hình thang ABCD( AB//CD) có hai đường chéo cắt nhau tại O. Đường thẳng qua O và song song với đáy AB cắt các cạnh bên AD,BC theo thứ tự M và N
a. Chứng minh rằng OM=ON
bChứng minh rằng 1/AB+1/CD=2/MN
c Biết SAOB=2010*2; SCOD= 2011*2. TÍNH sabcd
Cho hình thang ABCD (AB // CD). Hai đường chéo AC và BD cắt nhau tại O. Đường thẳng a qua O và song song với đáy của hình thang cắt các cạnh AD, BC theo thứ tự tại E và F (h.26).
Chứng minh rằng OE = OF
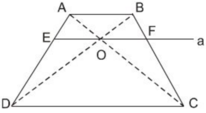
Cho hình thang ABCD (AB //CD). Hai đường chéo AC và BD cắt nhau tại O. Đường thẳng A qua O và song song với đáy của hình thang cắt các cạnh AD, BC theo thứ tự E và F
Chứng minh rằng OE = OF.
Cho hình thang ABCD (AB //CD) có hai đường chéo AC và BD cắt nhat tại O. Đường thẳng qua O và song song với đáy AB cắt các cạnh bên AD, BC theo thứ tự M và N
Chứng minh rằng:a) OA.OD=OB.OC
b)OM=ON