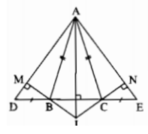
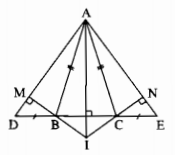
Bài 1: Cho ΔADE cân tại A. Trên cạnh DE lấy điểm B và C sao cho DB = EC < 1/2 DE.
a. ΔABC là tam giác gì? Hãy chứng minh điều đó.
b. Kẻ BM ⊥ AD, kẻ CN ⊥ AE. Hãy chứng minh BM = CN.\
c. Gọi I là giao điểm của MB và NC. ΔIBC là tam giác gì? Hãy chứng minh điều đó.
d. Chứng minh rằng AI là tia phân giác của góc BAC.