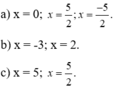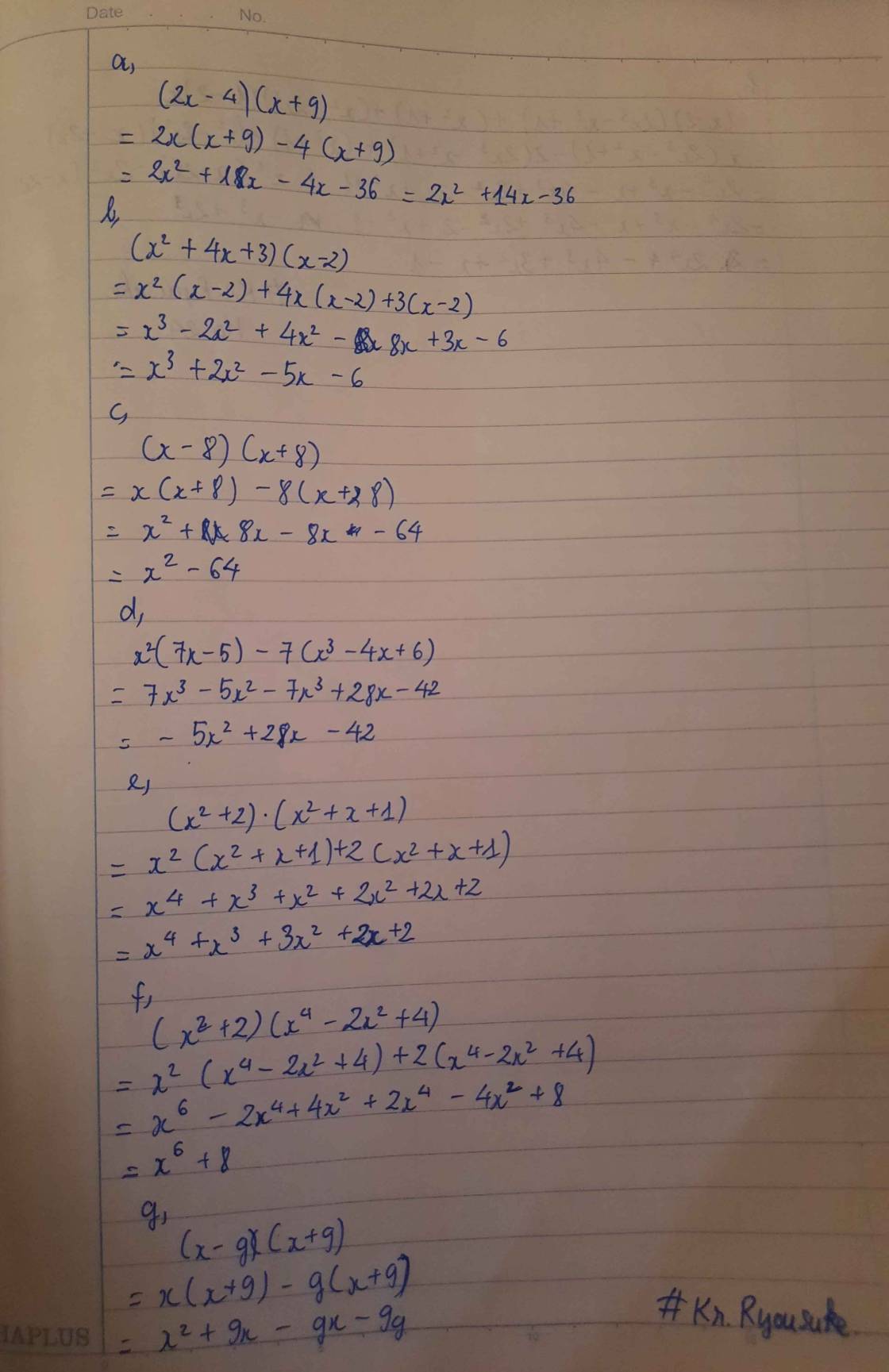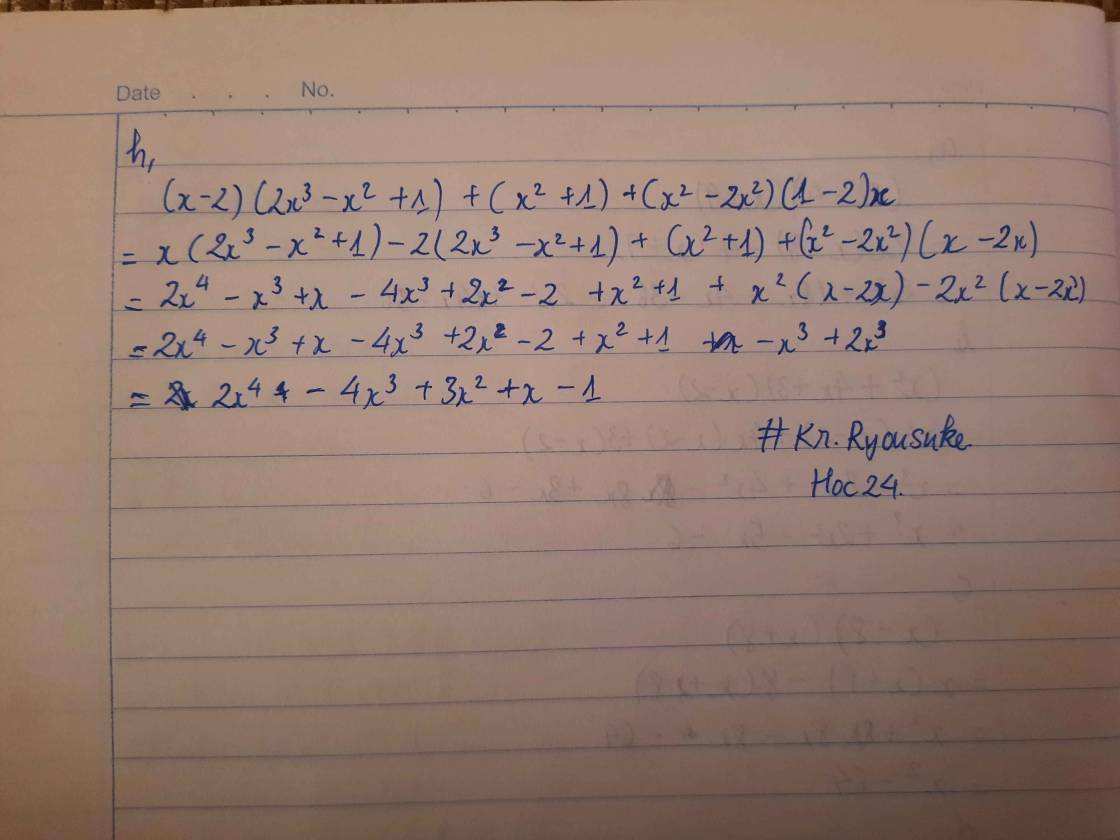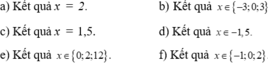2(x2−x+6)=5√x3+8.

Những câu hỏi liên quan
Tìm x, biết:a) 8
x
3
- 50x 0;b) 2(x + 3)-
x
2
- 3x 0;c) 6
x
2
- 15x - (2x - 5)(2x + 5) 0.
Đọc tiếp
Tìm x, biết:
a) 8 x 3 - 50x = 0;
b) 2(x + 3)- x 2 - 3x = 0;
c) 6 x 2 - 15x - (2x - 5)(2x + 5) = 0.
Bài 2: Tìm x, biết:
a) 4x(x + 1) = 8( x + 1) c) x2 – 6x + 8 = 0
b) x3 + x2 + x + 1 = 0 d) x3 – 7x – 6 = 0
\(a,\Leftrightarrow\left(4x-8\right)\left(x+1\right)=0\\ \Leftrightarrow4\left(x-2\right)\left(x+1\right)=0\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\\ b,\Leftrightarrow\left(x+1\right)\left(x^2+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-1\\x^2=-1\left(vô.lí\right)\end{matrix}\right.\Leftrightarrow x=-1\\ c,\Leftrightarrow x^2-2x-4x+8=0\\ \Leftrightarrow\left(x-2\right)\left(x-4\right)=0\Leftrightarrow\left[{}\begin{matrix}x=2\\x=4\end{matrix}\right.\\ d,\Leftrightarrow x^3-3x^2+3x-9x+2x-6=0\\ \Leftrightarrow\left(x-3\right)\left(x^2+3x+2\right)=0\\ \Leftrightarrow\left(x-3\right)\left(x^2+x+2x+2\right)=0\\ \Leftrightarrow\left(x-3\right)\left(x+1\right)\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=3\\x=-1\\x=-2\end{matrix}\right.\)
Đúng 1
Bình luận (0)
a) \(\Rightarrow4\left(x+1\right)\left(x-2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=-1\\x=2\end{matrix}\right.\)
b) \(\Rightarrow x^2\left(x+1\right)+\left(x+1\right)=0\)
\(\Rightarrow\left(x+1\right)\left(x^2+1\right)=0\)
\(\Rightarrow x=-1\left(do.x^2+1\ge1>0\right)\)
c) \(\Rightarrow x\left(x-4\right)-2\left(x-4\right)=0\)
\(\Rightarrow\left(x-4\right)\left(x-2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=4\\x=2\end{matrix}\right.\)
d) \(\Rightarrow x^2\left(x-3\right)+3x\left(x-3\right)+2\left(x-3\right)\)
\(\Rightarrow\left(x-3\right)\left(x^2+3x+2\right)=0\)
\(\Rightarrow\left(x-3\right)\left(x+1\right)\left(x+2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=3\\x=-2\\x=-1\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Xét sự đồng biến, nghịch biến của các hàm số:a) y 3
x
2
− 8
x
3
b) y 16x + 2
x
2
− 16
x
3
/3 −
x
4
c) y
x
3
− 6
x
2
+ 9xd) y
x
4
+ 8...
Đọc tiếp
Xét sự đồng biến, nghịch biến của các hàm số:
a) y = 3 x 2 − 8 x 3
b) y = 16x + 2 x 2 − 16 x 3 /3 − x 4
c) y = x 3 − 6 x 2 + 9x
d) y = x 4 + 8 x 2 + 5
a) TXĐ: R
y′ = 6x − 24 x 2 = 6x(1 − 4x)
y' = 0 ⇔ 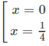
y' > 0 trên khoảng (0; 1/4) , suy ra y đồng biến trên khoảng (0; 1/4)
y' < 0 trên các khoảng ( - ∞ ; 0 ); (14; + ∞ ), suy ra y nghịch biến trên các khoảng ( - ∞ ;0 ); (14; + ∞ )
b) TXĐ: R
y′ = 16 + 4x − 16 x 2 − 4 x 3 = −4(x + 4)( x 2 − 1)
y' = 0 ⇔ 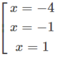
Bảng biến thiên:
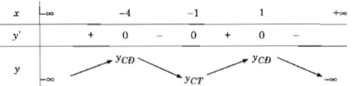
Vậy hàm số y đã cho đồng biến trên các khoảng ( - ∞ ; -4) và (-1; 1), nghịch biến trên các khoảng (-4; -1) và (1; + ∞ )
c) TXĐ: R
y′ = 3 x 2 − 12x + 9
y' = 0
y' > 0 trên các khoảng ( - ∞ ; 1), (3; + ∞ ) nên y đồng biến trên các khoảng ( - ∞ ; 1), (3; + ∞ )
y'< 0 trên khoảng (1; 3) nên y nghịch biến trên khoảng (1; 3)
d) TXĐ: R
y′ = 4 x 3 + 16 = 4x( x 2 + 4)
y' = 0 ⇔ 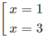
y' > 0 trên khoảng (0; + ∞ ) ⇒ y đồng biến trên khoảng (0; + ∞ )
y' < 0 trên khoảng ( - ∞ ; 0) ⇒ y nghịch biến trên khoảng ( - ∞ ; 0)
Đúng 0
Bình luận (0)
Thực hiện phép tính:
a,(2x- 4)(x+9)
b,(x2 + 4x +3)(x-2)
c,(x-8)(x+8)
d, x2(7x-5)-7(x3- 4x+6)
e,(x2+2)(x2+x+1)
f,(x2+2)(x4-2x2+4)
g,(x-g)(x+9)
h,(x-2)(2x3-x2+1)+(x2+1)+(x2-2x2)(1-2)x
Dễ
Thế
Mà
Cũnhoir
Dc
Ạ
Chịu
Chắc
Phải
Ngu
Lamqs
Mới
Hỏi
Câu
Này
Đúng 1
Bình luận (0)
Giải pt : a) 2/-x2+6x-8 - x-1/x-2 = x+3/x-4
b) 2/x3-x2-x+1 = 3/1-x2 - 1/x+1
c) x+2/x-2 - 2/x2-2x = 1/x
d) 5/-x2+5x-6 + x+3/2-x = 0
e) x/2x+2 - 2x/x2-2x-3 = x/6-2x
f) 1/x-1 - 3x2/x3-1 = 2x/x2+x-1
Tìm x biết:a)
x
6
+ 2
x
3
+1 0; b) x(x - 5) 4x - 20;c)
x
4
-2
x
2
8-4
x
2
; d) (
x
3
-
x
2
) - 4
x
2
+ 8x-4 0.
Đọc tiếp
Tìm x biết:
a) x 6 + 2 x 3 +1 = 0; b) x(x - 5) = 4x - 20;
c) x 4 -2 x 2 =8-4 x 2 ; d) ( x 3 - x 2 ) - 4 x 2 + 8x-4 = 0.
a) x = -1. b) x = 4 hoặc x = 5.
c) x = ± 2 . d) x = 1 hoặc x = 2.
Đúng 0
Bình luận (0)
Bài 2: Phân tích thành nhân tử:b) (x+2)2-25c) 36(x-y)2d) x2+1/2x+1/16e) 2x4y3-3x2y4+5x3y4f) 3x(x-2)+5(2-x)g) 3x(x-2y)+6y(2y-x)i) x(x-1)+(1-x)2k) 2y(x+2)-3x-6l) x2+6x-3(x+6)m) xy+x-2y-2n) 3x2-3xy-5x+5y15) x3-8/12516) x2-x-y2-yy17) x3+4x-(y3+4y)18) 5x-√5x+1/419) x3+2x2+x-16xy220) (x+2y)2-(x-y)21) (9x2-33x3x+2y+-4y222) 9x2-6xy+3x-y+y2
Đọc tiếp
Bài 2: Phân tích thành nhân tử:
b) (x+2)2-25
c) 36(x-y)2
d) x2+1/2x+1/16
e) 2x4y3-3x2y4+5x3y4
f) 3x(x-2)+5(2-x)
g) 3x(x-2y)+6y(2y-x)
i) x(x-1)+(1-x)2
k) 2y(x+2)-3x-6
l) x2+6x-3(x+6)
m) xy+x-2y-2
n) 3x2-3xy-5x+5y
15) x3-8/125
16) x2-x-y2-yy
17) x3+4x-(y3+4y)
18) 5x-√5x+1/4
19) x3+2x2+x-16xy2
20) (x+2y)2-(x-y)
21) (9x2-33x3x+2y+-4y2
22) 9x2-6xy+3x-y+y2
\(b,\left(x+2\right)^2-25\)
\(=\left(x+2\right)^2-5^2\)
\(=\left(x-3\right)\left(x+7\right)\)
\(c,36\left(x-y\right)^2\)
\(=36\left(x^2-2xy+y^2\right)\)
\(=36x^2-72xy+36y^2\)
\(d,x^2+\dfrac{1}{2}x+\dfrac{1}{16}\)
\(=x^2+2.x.\dfrac{1}{4}+\dfrac{1}{4}^2\)
\(=\left(x+\dfrac{1}{4}\right)^2\)
\(e,2x^4y^3-3x^2y^4+5x^3y^4\)
\(=x^2y^3\left(2x^2-3y+5xy\right)\)
Các câu còn lại làm tương tự, chú ý sd HĐT
Đúng 1
Bình luận (1)
1) x3-x2+2x-2 4) ax-2x-a2+2a 7) x2-6xy-25z2+9y2
2) x2-y2+2x+2y 5) 2xy +3z+6y+xz 8) x3-2x2+x
3) x2/4+2xy+4y2-25 6) x2y2+yz+y3+zx2 9) x4+4
Tìm x, biết:a) 2-x 2
(
x
-
2
)
3
; b) 8
x
3
- 72x 0;c)
(
x
-
1
,
5
)
6
+
...
Đọc tiếp
Tìm x, biết:
a) 2-x = 2 ( x - 2 ) 3 ; b) 8 x 3 - 72x = 0;
c) ( x - 1 , 5 ) 6 + 2 ( 1 , 5 - x ) 2 = 0; d) 2 x 3 +3 x 2 +3 + 2x = 0;
e) x 3 - 4x- 14x(x - 2) = 0; g) x 2 (x + 1)- x(x + 1) + x(x - 1) = 0.