Áp dụng tính chất tổng ba góc trong 1 tam giác vào tam giác ABC, có:

\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\Rightarrow\widehat{B}=180^0-60^0-50^0=70^0\)

Vì BD là tia phân giác của góc B => \(\widehat{ABD}=\widehat{DBC}=\frac{70^0}{2}=35^0\)

Áp dụng tính chất tổng ba góc trong 1 tam giác vào tam giác ADB, có:

\(\widehat{ABD}+\widehat{A}+\widehat{ADB}=180^0\Rightarrow\widehat{ADB}=85^0\)

\(\Rightarrow\widehat{BDC}=180^0-\widehat{ADB}=95^0\)( Do chúng là 2 góc kề bù )

Vậy...

~~ Chắc chắn đúng cậu nhé ~ Tiếc gì 1 tk cho tớ nào?

Ta có hình vẽ:

Xét Δ ABC có: ABC + C + A = 180^o

=> ABC + 50^o + 60^o = 180^o

=> ABC + 110^o = 180^o

=> ABC = 180^o - 110^o = 70^o

Vì BD là phân giác của ABC nên B₁ = B₂ = \(\frac{ABC}{2}=\frac{70^o}{2}=35^o\)

=> 60^o + ADB + 35^o = 180^o

=> 95^o + ADB = 180^o

=> ADB = 180^o - 95^o = 85^o

=> 85^o + CDB = 180^o

=> BDC + 85^o = 180^o

=> BDC = 180^o - 85^o = 95^o

Xét tam giác ABC có:

 góc ABC+góc ACB+góc BAC=180⁰(định lí....)

=>góc ABC=180⁰-(góc ACB+góc BAC)=180⁰-(50⁰+60⁰)=180⁰-110⁰=70⁰

Vì BD là tia phân giác của góc ABC (gt)

=>góc ABD=góc CBD=góc ABC/2=70⁰/2=35⁰

Xét tam giác ABD có:

góc BAD+góc ABD+góc ADB=180⁰ (đ/lí...)

=>góc ADB=180⁰-(góc BAD+góc ABD)=180⁰-(60⁰+35⁰)=85⁰

Xét tam giác CBD có:

góc BCD+góc CDB+góc CBD=180⁰ (đ/lí...)

=>góc CDB=180⁰-(góc BCD+góc CBD)=180⁰-(50⁰+35⁰)=95⁰

Vậy.................

góc ABC=180-50-60=70

góc ABD=góc CBD=góc B:2=70:2=35

Ta có: góc ADB+ góc ABD+góc A=180*( tổng 3 góc trong 1 tam giác)

=>góc ADB=180*- góc ABD-góc A

góc ADB=180-35-60=85

Tương tự 

 CDB+ góc CBD+góc C=180*( tổng 3 góc trong 1 tam giác)

=>góc CDB=180*- góc CBD-góc C

góc CDB=180-35-50=95

Ta có: \(\widehat{CAB}+\widehat{CBA}+\widehat{BCA}=180\Rightarrow\widehat{CBA}=180-\widehat{CAB}-\widehat{BCA}\Rightarrow\widehat{CBA}=180-50-60=70\)

Do: \(\widehat{CBD}+\widehat{DBA}=\widehat{CBA}\Rightarrow\widehat{CBD}+\widehat{DBA}=70\)mà\(\widehat{CBD}=\widehat{DBA}\)

\(\Rightarrow\widehat{CBD}=\widehat{DBA}=35\)

Trong tam giác ABD có:\(\widehat{BAD}+\widehat{ABD}+\widehat{ADB}=180\Rightarrow\widehat{ADB}=180-\widehat{BAD}-\widehat{ABD}\Rightarrow\widehat{ADB}=180-35-60=85\)

Trong tam giác BCD có: 

\(\widehat{CBD}+\widehat{BCD}+\widehat{CDB}=180\Rightarrow\widehat{CDB}=180-\widehat{CBD}-\widehat{BCD}\Rightarrow\widehat{CDB}=180-35-50=95\)

(Mình không ghi được kí hiệu độ nên bạn để ý thêm vào bài nhé)

Xét tam giác ABC 

có ^A+^B+^C=180

Thay 60+^b+50=180

=>^B=180-60-50=70 độ

Xét tam giác ABD có

^A+^D+^B=180

THAY 60+d+70:2=180

=>d= 85 

tìm cdb tương tự

góc ABC=180-60-50=70 độ

=>góc ABD=góc CBD=70/2=35 độ

góc BDC=35+60=95 độ

góc ADB=180-95=85 độ

Giải

Ta có: tam giác ABC: A + B + C = 180 ( định lý )

                         60 + B + 50  = 180

                        B + 110         = 180

                        B                  = 180 - 110

                        B                  = 70

Ta có: B = B1 + B2 ( theo hình mk vẽ và đặt tên)

=> B = 70 => B1 = B2 = 35

Ta có: B1 + A = ADB ( t chất góc ngoài )

35 + 60 = ADB

=> ADB = 95

Mặt khác B2 + C  = BDC ( T chất góc ngoài )

35 + 50 = BDC

=> BDC = 85

Vậy .......

 Thêm dấu góc nha, mk

tam giác abc có góc a+b+c=180 đọ (tổng các góc trong của tam giác )

\(\Rightarrow b=180-60-50=70\)

\(b1=b2=\frac{70}{2}=35\)

\(b1+A+ADB=180\)(Tổng các góc trong 1 tam giác)

\(\Rightarrow ADB=180-60-35=85\)

CDB+ADB=180(2 góc kề bù)

\(\Rightarrow CDB=180-85=95\)

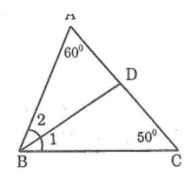
Trong ΔABC ta có:

∠A + ∠B + ∠C = 180o(tổng ba góc trong tam giác)

⇒∠B = 180o - (∠A +∠C )

⇒x = 180o - (60o + 50o) = 70o

(∠B1) =(∠B2 ) = (1/2 )∠B (vì BD là tia phân giác)

⇒ ∠B1 = ∠B2 = 70o : 2 = 35o

Trong ΔBCD ta có ∠(ADB) là góc ngoài tại đỉnh D

⇒ ∠(ADB) = ∠(B1 ) + ∠C (tính chất góc ngoài tam giác)

Nên ∠(ADB) = 35º + 50º = 85º

+) Do ∠(ADB) + ∠(BDC) = 180o(hai góc kề bù)

⇒∠(BDC) = 180o-∠(ADB) = 180o - 85o = 95o