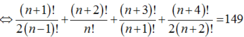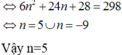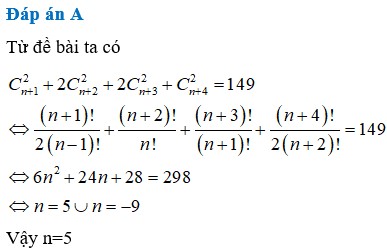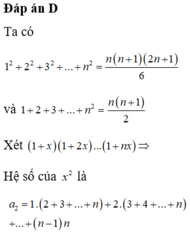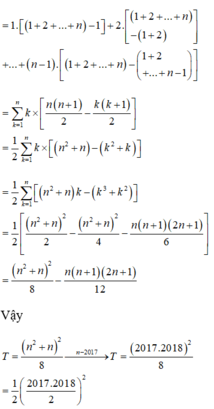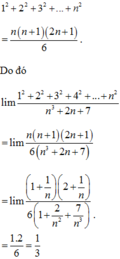Giá trị biểu thức M = 12 - 22 + 32 - 42 ... - 20162 + 20172

Những câu hỏi liên quan
Tính giá trị của biểu thức
M
A
n
+
1
4
+
3
A
n
3
(
n
+
1
)...
Đọc tiếp
Tính giá trị của biểu thức M = A n + 1 4 + 3 A n 3 ( n + 1 ) ! biết rằng C n + 1 2 + 2 C n + 2 2 + 2 C n + 3 2 + C n + 4 2 = 149
A. 3 4
B. 4 3
C. 15 9
D. 17 25
Tính giá trị của biểu thức
M
A
n
+
1
4
+
3
A
n
3
(
n
+
1
)
!
biết rằng ...
Đọc tiếp
Tính giá trị của biểu thức M = A n + 1 4 + 3 A n 3 ( n + 1 ) ! biết rằng C n + 1 2 + 2 C n + 2 2 + 3 C n + 3 2 + 4 C n + 4 2 = 149
A. M = 3 4
B. M = 4 3
C. M = 15 9
D. M = 17 25
Tính giá trị của biểu thức:
A
A
n
+
1
4
+
3
A
n
3
n
+
1
!
. Biết rằng: ...
Đọc tiếp
Tính giá trị của biểu thức: A = A n + 1 4 + 3 A n 3 n + 1 ! . Biết rằng: C n + 1 2 + 2 C n + 2 2 + 2 C n + 3 2 + C n + 4 2 = 149
A. 4 3
B. 3 4
C. 5 4
D. 4 5
Cho khai triển
P
x
1
+
x
1
+
2
x
.
.
.
1
+
2017
x...
Đọc tiếp
Cho khai triển P x = 1 + x 1 + 2 x . . . 1 + 2017 x = a 0 + a 1 x + . . . + a 2017 x 2017 .
Tính giá trị biểu thức T = a 2 + 1 2 1 2 + 2 2 + . . . + 2017 2
A. 2016 . 2017 2 2
B. 2017 . 2018 2 2
C. 1 2 . 2016 . 2017 2 2
D. 1 2 . 2017 . 2018 2 2
Cho khai triển:
P
x
1
+
x
1
+
2
x
..
1
+
2017
x
a
0
+
a
1
x
+
..
+
a...
Đọc tiếp
Cho khai triển:
P x = 1 + x 1 + 2 x .. 1 + 2017 x = a 0 + a 1 x + .. + a 2017 x 2017 .
Tính giá trị biểu thức T = a 2 + 1 2 1 2 + 2 2 + ... + 2017 2 .
A. 2016.2017 2 2
B. 2017.2018 2 2
C. 1 2 . 2016.2017 2 2
D. 1 2 . 2017.2018 2 2
Đáp án D
Ta có 1 2 + 2 2 + 3 2 + ... + n 2 = n n + 1 2 n + 1 6
và 1 + 2 + 3 + ... + n 2 = n n + 1 2
Xét 1 + x 1 + 2 x ... 1 + n x ⇒ Hệ số của x 2 là
a 2 = 1. 2 + 3 + ... + n + 2. 3 + 4 + ... + n + ... + n − 1 n
= 1. 1 + 2 + ... + n − 1 + 2. 1 + 2 + ... + n − 1 + 2 + ... + n − 1 . 1 + 2 + ... + n − 1 + 2 + ... + n − 1
= ∑ k = 1 n k × n n + 1 2 − k k + 1 2
= 1 2 ∑ k = 1 n k × n 2 + n − k 2 + k
= 1 2 ∑ k = 1 n n 2 + n k − k 3 + k 2
= 1 2 = n 2 + n 2 8 − n n + 1 2 n + 1 12
n 2 + n 2 2 − n 2 + n 2 4 − n n + 1 2 n + 1 6
Vậy T = n 2 + n 2 8
→ n − 2017 T = 2017.2018 2 8 = 1 2 2017.2018 2 2
Đúng 0
Bình luận (0)
Cho
M
77
2
+
75
2
+
73
2
+
…
+
3
2
+
1
2
và
N
76
2...
Đọc tiếp
Cho M = 77 2 + 75 2 + 73 2 + … + 3 2 + 1 2
và N = 76 2 + 74 2 + … + 2 2
Tính giá trị của biểu thức M - N - 3 3000
A. 10
B. 30
C. 1
D. 100
Xét
M – N = 77 2 + 75 2 + 73 2 + … + 3 2 + 1 2 – ( 76 2 + 74 2 + … + 2 2 ) = ( 77 2 – 76 2 ) + ( 75 2 – 74 2 ) + ( 73 2 – 71 2 ) + … + ( 3 2 – 2 2 ) + 1 2
= (77 + 76)(77 – 76) + (75 + 74)(75 – 74) + … + (3 + 2)(3 – 2) + 1
= (77 + 76).1 + (75 + 74).1 + … + (3 + 2).1 + 1
= 77 + 76 + 75 + 74 + 73 + … + 3 + 2 + 1
= 77 + 1 2 . 77 = 3003
Từ đó M - N - 3 3000 = 3003 - 3 3000 = 3000 3000 = 1
Đáp án cần chọn là: C
Đúng 0
Bình luận (0)
Cho biết:
1
2
+
2
2
+
3
2
+
.
.
.
+
10
2
385
Tính nhanh giá trị của biểu thức sau
S
12
2
+
14...
Đọc tiếp
Cho biết: 1 2 + 2 2 + 3 2 + . . . + 10 2 = 385
Tính nhanh giá trị của biểu thức sau S = 12 2 + 14 2 + 16 2 + 18 2 + 20 2 - 1 2 + 3 2 + 5 2 + 7 2 + 9 2
A. 1155
B. 5511
C. 5151
D. 1515
Giới hạn lim
1
2
+
2
2
+
3
2
+
4
2
+
.
.
.
+
n...
Đọc tiếp
Giới hạn lim 1 2 + 2 2 + 3 2 + 4 2 + . . . + n 2 n 3 + 2 n + 7 có giá trị bằng?
A. 2 3 .
B. 1 6 .
C. 0.
D. 1 3 .
cho biểu thức:
A= (-12) mũ 8, B= (-55). (-47). (-32). (-21), C= (--65). (-43).(-22), D= (-11) mũ 5
Những biểu thức có giá trị lớn hơn 0 là?
A,B là các biểu thức dương
Đúng 0
Bình luận (0)
Cho a, b, c, d, e, f là các số thực thỏa mãn
(
d
-
1
)
2
+
e
-
2
2...
Đọc tiếp
Cho a, b, c, d, e, f là các số thực thỏa mãn
( d - 1 ) 2 + e - 2 2 + f - 3 2 = 1 a + 3 2 + b - 2 2 + c 2 = 9
Gọi giá trị lớn nhất, giá trị nhỏ nhất của biểu thức F = a - d 2 + b - e 2 + c - f 2 lần lượt là M, m
Khi đó, M - m bằng:
A. 10
B. 10
C. 8
D. 2 2
Chọn C
Gọi A (d; e; f) thì A thuộc mặt cầu (S1): (x - 1)2 + (y - 2)2 + (z- 3)2 = 1 có tâm I1 = (1; 2; 3), bán kính R1 = 1
B (a; b; c) thì B thuộc mặt cầu (S2): (x - 3)2 + (y - 2)2 + z2 = 9 có tâm I2 = (-3; 2; 0), bán kính R2 = 3
Ta có I1I2 = 5 > R1 + R2 => (S1) và (S2) không cắt nhau và ở ngoài nhau.
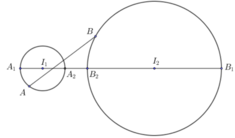
Dễ thấy F = AB, AB max khi A ≡ A1; B ≡ B1
=> Giá trị lớn nhất bằng I1I2 + R1 + R2 = 9.
AB min khi A ≡ A2; B ≡ B2
=> Giá trị nhỏ nhất bằng I1I2 - R1 - R2 = 1.
Vậy M - m =8
Đúng 0
Bình luận (0)