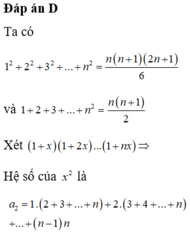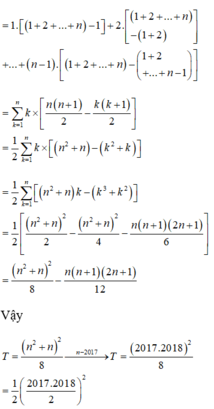Các câu hỏi tương tự
Cho khai triển: \(\left(1+x+x^2+...+x^{2015}\right)^{2016}=a_0+a_1x+a_2x^2+...+a_{4062240}x^{4062240}\). Tính giá trị biểu thức: \(T=C^0_{2016}a_{2016}-C^1_{2016}a^{2015}+C^2_{2016}a_{2014}-...+C^{2016}_{2016a_{ }0}\)
Tìm giá trị của tổng \(S=C_{2017}^0+\dfrac{1}{2}C_{2017}^1+\dfrac{1}{3}C_{2017}^2+...+\dfrac{1}{2018}C_{2017}^{2017}\)
Sử dụng nhị thức newton triển khai các biểu thức sau:
a) (2-3x)5
b) [x-(2/x2 )]4
c) (a-√2)⁶
d)(x-1/x)¹³
Cảm ơn :>>
a) tính gtrị của biểu thức A = \(\sqrt{3}+\sqrt{12}-\sqrt{27}-\sqrt{36}\)
b) cho bt B = \(\dfrac{2}{\sqrt{x-1}}-\dfrac{1}{\sqrt{x}}+\dfrac{3\sqrt{x-5}}{\sqrt{x\left(\sqrt{x-1}\right)}}\) với x > 0 và x \(\ne\) 1 . rút gọn bt và tìm x để B = 2
Limx->1 (\(\frac{2017}{1-x^{2017}}-\frac{2018}{1-x^{2018}}\) )
Cho biểu thức
P
x
+
1
x
2
3
-
x
+
1...
Đọc tiếp
Cho biểu thức P = x + 1 x 2 3 - x + 1 3 - x - 1 x - x 10 với x>0, x ≠ 1. Tìm số hạng không chứa x trong khai triển nhị thức Newton của P.
A. 200
B. 100
C. 210
D. 160
Cho biết : \(\lim\limits_{x\rightarrow1}\dfrac{\sqrt{ax^2+1}-bx-2}{x^3-3x+2}\left(a,b\in R\right)\) có kết quả là một số thực. Giá trị của biểu thức \(a^2+b^2\) ?
Cho biểu thức: P(x)
(
1
+
x
)
9
+
(
1
+
x
)
10
+
(
1
+
x
)
11
+...
Đọc tiếp
Cho biểu thức: P(x) = ( 1 + x ) 9 + ( 1 + x ) 10 + ( 1 + x ) 11 + ( 1 + x ) 12 + ( 1 + x ) 13 + ( 1 + x ) 14 + ( 1 + x ) 15 . Hệ số của số hạng chứa x 9 trong khai triển thành đa thức của P(x) là
A. 3003
B. 8000
C. 8008
D. 3000
Cho a,b là các số thực và hàm số
f
x
x
-
a
-
1
x
2
-
4...
Đọc tiếp
Cho a,b là các số thực và hàm số f x = x - a - 1 x 2 - 4 k h i x ≠ 2 2 x - b k h i x = 2 liên tục tại x=2. Tính giá trị của biểu thức T=a+b.
A. T= 31 8
B. T=5
C. T=3
D. T= 39 8
Gọi `bb A` là giới hạn của hàm số `f(x)=[x+x^2+x^3+...+x^50 -50]/[x-1]` khi `x -> 1.` Tính giá trị của `bb A.`