giải phương trình
4(x+5)(x+6)(x+10)(x+12) = 3x2
Giúp vs ạ
Bài 1 giải các bất phương trình sau
a.x2 - x - 6 = 0
b.2x2 - 7x + 5 < 0
c.3x2 - 9x + 6 ≥ 0
d.2x2 - 5x + 3 < 0
Bài 2 Giải phương trình sau
A.√x2 + x + 5 = √2x2 - 4x + 1
B.√11x2 -14x - 12 = √3x2 + 4x - 7
Bài 2:
a: =>2x^2-4x+1=x^2+x+5
=>x^2-5x-4=0
=>\(x=\dfrac{5\pm\sqrt{41}}{2}\)
b: =>11x^2-14x-12=3x^2+4x-7
=>8x^2-18x-5=0
=>x=5/2 hoặc x=-1/4
Giải phương trình bằng cách đưa về phương trình tích:
a ) 3 x 2 − 7 x − 10 ⋅ 2 x 2 + ( 1 − 5 ) x + 5 − 3 = 0 b ) x 3 + 3 x 2 − 2 x − 6 = 0 c ) x 2 − 1 ( 0 , 6 x + 1 ) = 0 , 6 x 2 + x d ) x 2 + 2 x − 5 2 = x 2 − x + 5 2
a) 3 x 2 − 7 x − 10 ⋅ 2 x 2 + ( 1 − 5 ) x + 5 − 3 = 0
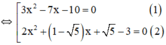
+ Giải (1):
3 x 2 – 7 x – 10 = 0
Có a = 3; b = -7; c = -10
⇒ a – b + c = 0
⇒ (1) có hai nghiệm x 1 = - 1 v à x 2 = - c / a = 10 / 3 .
+ Giải (2):
2 x 2 + ( 1 - √ 5 ) x + √ 5 - 3 = 0
Có a = 2; b = 1 - √5; c = √5 - 3
⇒ a + b + c = 0
⇒ (2) có hai nghiệm:
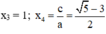
Vậy phương trình có tập nghiệm 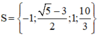
b)
x 3 + 3 x 2 - 2 x - 6 = 0 ⇔ x 3 + 3 x 2 - ( 2 x + 6 ) = 0 ⇔ x 2 ( x + 3 ) - 2 ( x + 3 ) = 0 ⇔ x 2 - 2 ( x + 3 ) = 0
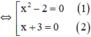
+ Giải (1): x 2 – 2 = 0 ⇔ x 2 = 2 ⇔ x = √2 hoặc x = -√2.
+ Giải (2): x + 3 = 0 ⇔ x = -3.
Vậy phương trình có tập nghiệm S = {-3; -√2; √2}
c)
x 2 − 1 ( 0 , 6 x + 1 ) = 0 , 6 x 2 + x ⇔ x 2 − 1 ( 0 , 6 x + 1 ) = x ⋅ ( 0 , 6 x + 1 ) ⇔ x 2 − 1 ( 0 , 6 x + 1 ) − x ( 0 , 6 x + 1 ) = 0 ⇔ ( 0 , 6 x + 1 ) x 2 − 1 − x = 0
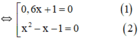
+ Giải (1): 0,6x + 1 = 0 ⇔ 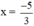
+ Giải (2):
x 2 – x – 1 = 0
Có a = 1; b = -1; c = -1
⇒ Δ = ( - 1 ) 2 – 4 . 1 . ( - 1 ) = 5 > 0
⇒ (2) có hai nghiệm 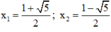
Vậy phương trình có tập nghiệm 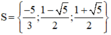
d)
x 2 + 2 x − 5 2 = x 2 − x + 5 2 ⇔ x 2 + 2 x − 5 2 − x 2 − x + 5 2 = 0 ⇔ x 2 + 2 x − 5 − x 2 − x + 5 ⋅ x 2 + 2 x − 5 + x 2 − x + 5 = 0 ⇔ ( 3 x − 10 ) 2 x 2 + x = 0
⇔ (3x-10).x.(2x+1)=0
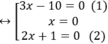
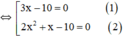
+ Giải (1): 3x – 10 = 0 ⇔ 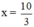
+ Giải (2):
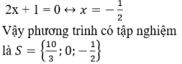
Giải các phương trình sau:
a) 4 x − 5 = x + 7 ; b) 10 x − 12 − 3 x = 6 + x ;
c) 5 x − 4 3 = 2 + 3 x 2 d) 7 x − 1 6 + 2 x = 16 − x 5 .
Phân tích đa thức thành nhân tử : 4(x + 5)(x + 6)(x + 10)(x + 12) + 3x2
Đa thức này không phân tích được thành nhân tử.
Bạn coi lại đề.
Ta có: \(4\left(x+5\right)\left(x+6\right)\left(x+10\right)\left(x+12\right)+3x^2\)
\(=4\left(x^2+60+17x\right)\left(x^2+60x+16x\right)+3x^2\)
\(=4\left[\left(x^2+60\right)^2+33x\left(x^2+60\right)+272x^2\right]+3x^2\)
\(=4\left(x^2+60\right)^2+132x\left(x^2+60\right)+1091x^2\)
Giải các phương trình sau:
a) 2 x + 1 2 − 2 x − 1 = 2 ;
b) x 2 − 3 x 2 + 5 x 2 − 3 x + 6 = 0 ;
c) x 2 − x − 1 x 2 − x − 2 = 0 .
giải phương trình 4(x+5)(x+6)(x+10)(x+12)=3x^2
Xét x=0 ==> loại
Xét x\(\ne\)0,ta chia cả 2 vế cho x2 thu được:
4(x2+17x+60)(x2+16x+60)=3x2
4(x+\(\frac{60}{x}\)+17)(x+\(\frac{60}{x}\)+16)=3
Đặt x+\(\frac{60}{x}\)+16=t,ta được
4(t+1).t=3 <=> 4t2+4t-3=0 <=> t=\(\frac{1}{2}\)hoặc t=\(\frac{-3}{2}\)
Với t=1/2,ta có x+\(\frac{60}{x}\)+16=1/2 <=> x=-15/2 hoặc x=-8
Với t=-3/2,ta có x+\(\frac{60}{x}\)+16=-3/2 <=> ... bạn tự giải nốt nhé.
Giải các phương trình sau:
a) 5 − 2 x 2 + 4 x − 10 = 8 ;
b) x 2 + 2 x + 3 x 2 + 2 x + 1 = 3 ;
c) x x − 1 x 2 − x + 1 − 6 = 0 .
Giải phương trình
4(x+5)(x+6)(x+10)(x+12)=0
Ta có: \(4\left(x+5\right)\left(x+6\right)\left(x+10\right)\left(x+12\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+5=0\\x+6=0\\x+10=0\\x+12=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=-5\\x=-6\\x=-10\\x=-12\end{matrix}\right.\)
Vậy \(x\in\left\{-5;-6;-10;-12\right\}\)
Bài 5: Giải các phương trình sau:
a. (3x - 1)2 - (x + 3)2 = 0
b. x3 = \(\dfrac{x}{49}\)
c. x2 - 7x + 12 = 0
d. 4x2 - 3x -1 = 0
e. x3 - 2x - 4 = 0
f. x3 + 8x2 + 17x +10 = 0
g. x3 + 3x2 + 6x + 4 = 0
h. x3 - 11x2 + 30x = 0
a. (3x - 1)2 - (x + 3)2 = 0
\(\Leftrightarrow\left(3x-1+x+3\right)\left(3x-1-x-3\right)=0\)
\(\Leftrightarrow\left(4x+2\right)\left(2x-4\right)=0\)
\(\Leftrightarrow4x+2=0\) hoặc \(2x-4=0\)
1. \(4x+2=0\Leftrightarrow4x=-2\Leftrightarrow x=-\dfrac{1}{2}\)
2. \(2x-4=0\Leftrightarrow2x=4\Leftrightarrow x=2\)
S=\(\left\{-\dfrac{1}{2};2\right\}\)
b. \(x^3=\dfrac{x}{49}\)
\(\Leftrightarrow49x^3=x\)
\(\Leftrightarrow49x^3-x=0\)
\(\Leftrightarrow x\left(49x^2-1\right)=0\)
\(\Leftrightarrow x\left(7x+1\right)\left(7x-1\right)=0\)
\(\Leftrightarrow x=0\) hoặc \(7x+1=0\) hoặc \(7x-1=0\)
1. x=0
2. \(7x+1=0\Leftrightarrow7x=-1\Leftrightarrow x=-\dfrac{1}{7}\)
3. \(7x-1=0\Leftrightarrow7x=1\Leftrightarrow x=\dfrac{1}{7}\)
*Cách khác:
a) Ta có: \(\left(3x-1\right)^2-\left(x+3\right)^2=0\)
\(\Leftrightarrow\left(3x-1\right)^2=\left(x+3\right)^2\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-1=-x-3\\3x-1=x+3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}4x=-2\\2x=4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=2\end{matrix}\right.\)
Vậy: \(S=\left\{-\dfrac{1}{2};2\right\}\)