Vẽ tam giác ABC có A =70 ; B và C là hai góc nhọn. Dùng eeke vẽ BD vuông góc với AC ( D ϵ AC ), Vẽ CE vuông góc với AB ( E ϵ AB ). Gọi H là giao điểm của BD và CE. Dùng thước đo góc xác định số đo các góc ABD, ACE, BHC.
giải nhanh giúp m với ạ
Những câu hỏi liên quan
Vẽ tam giác ABC có BC=4cm, góc B=70 độ, góc A=50 độ
Cho tam giác ABC có góc A=70 độ, H là trực tâm tam giác đó. VẼ điểm K đối xứng vs H qa BC:
a) C/m tam giác BKC= tam giác BHC.
b) Tính góc BKC
a : Gọi O là giao của HK và CB, ta có:
S của tam giác CHB= \(\frac{1}{2}OH\cdot CB\)
S của tam giác BKC=\(\frac{1}{2}KO\cdot CB\)
Mà ta có K là điểm đối xứng với H qua BC => KO=HO
Nên ta có thể thay
S của tam giác BKC=\(\frac{1}{2}OH\cdot CB\)
Hay \(Sbkc=Sbhc\)
Nếu đúng thì cho mk xin **** nha
Đúng 0
Bình luận (0)
cho tam giác ABC có góc B bằng góc C bằng 70 độ. Góc CAD là góc ngoài đỉnh A của tam giác ABC. Vẽ tia phân giác AM của góc CAD. Tính góc BAC. chứng minh AM song song BC
Áp dụng định lí tổng 3 góc trong 1 tam giác vào tam giác ABC,ta có:
góc BAC +góc B +góc C =180 độ
góc BAC + 70 độ + 70 độ =180 độ (do góc B = góc C = 70 độ)
góc BAC = 40 độ
Ta có: góc BAC +góc CAD =180 độ
40 độ + góc CAD = 180 độ (vì góc BAC = 40 độ )
góc CAD =140 độ
AM là tia phân giác của góc CAD (gt) nên góc CAM = 1/2 góc CAD = 1/2 .140= 70 (độ)
Do đó: góc CAM = góc C (= 70 độ )
Mà 2 góc này ở vị trí so le trong
Suy ra: AM song song với BC
Vậy AM song song với BC
Đúng 0
Bình luận (0)
cho tam giác ABC có góc B = 70 độ , góc C = 50 độ ( vẽ hình )
a) Tính số đo góc A
b) Vẽ tia phan giác của góc A cắt BC . tính góc AEB và góc AEC
1. Vẽ tam giác ABC có góc ngoài CBx. Giả sử CBx = 110 và A = 55. So sánh A và C
2. Vẽ tam giác ABC có B = C rồi vẽ góc ngoài CAx. Gọi At là tia phân giác cuae CAx. Giả sử B = C = 70
a. Chứng minh BAx = 2B
b. vẽ tia phân giác của BAx. So sánh BAt và B rồi cho nhận xét
3. Vẽ tam giác ABC với 2 góc ngoài ABx và ACy. Giả sử ABx = 130, ACy = 110
a. Tính ACB
b. Tính A
Cho tam giác ABC có A= 180 độ - 3C và B=70 độ
a) Tính số đo góc A và C của tam giác ABC;
b) Vẽ tia phân giác của góc B cắt AC tại E. Qua E kẻ đường thẳng song song với BC cắt AB tại D.
\(a,\widehat{A}+\widehat{B}+\widehat{C}=180\\ \Rightarrow180-3\widehat{C}+\widehat{C}+70=180\\ \Rightarrow-2\widehat{C}=-70\\ \Rightarrow\widehat{C}=35\\ \Rightarrow\widehat{A}=180-35=145\)
Đúng 3
Bình luận (0)
Cho tam giác ABC có ABC = 70, ACB = 40. Vẽ tia Cx là tia đối của tia CB. Vẽ tia Cy là phân giác của góc ACx
a. Tính ACx, xCy
b. Chứng minh rằng AB // Cy
a, Ta có: góc ACB + góc ACx = 180 độ (kề bù)
=>góc ACx = 180 độ - 40 độ = 140 độ
=>\(\widehat{xCy}=\widehat{ACy}=\frac{\widehat{ACx}}{2}=\frac{140^o}{2}=70^o\) (vì Cy là tia p/g của góc ACx)
b, Ta thấy \(\widehat{ABC}=\widehat{xCy}=70^o\)
Mà góc ABC và góc xCy là cặp góc đồng vị
=> AB // Cy
Đúng 4
Bình luận (0)
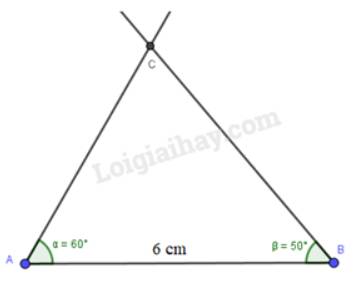
a) Em hãy trình bày các bước dùng phần mềm GeoGebra để vẽ tam giác ABC có:
AB = 6 cm, \(\widehat {BAC} = 60^\circ ,\widehat {ACB} = 70^\circ \)
b) Vẽ tam giác trên trong phần mềm GeoGebra và lưu thành một tệp có đuôi png
a) Xét tam giác ABC, áp dụng định lí tổng 3 góc trong tam giác, ta có:
\(\begin{array}{l}\widehat {BAC} + \widehat {ABC} + \widehat {ACB} = 180^\circ \\ \Rightarrow \widehat {ABC} = 180^\circ - (\widehat {BAC} + \widehat {ACB}) = 180^\circ - (60^\circ + 70^\circ ) = 50^\circ \end{array}\)
Bước 1: Vẽ AB = 6 cm
Bước 2: Vẽ \(\widehat {BAB'} = 60^\circ \)bằng cách:
Chọn công cụ Góc, nháy chuột lần lượt vào các điểm B, A ( theo chiều ngược kim đồng hồ) nhập số đo góc 60
Bước 3: Vẽ \(\widehat {ABA'} = 50^\circ \) bằng cách:
Chọn công cụ Góc, nháy chuột lần lượt vào các điểm A,B ( theo chiều kim đồng hồ) nhập số đo góc 50
Bước 4: Vẽ điểm C là giao điểm của AB’ và BA’
b)
Nháy chuột vào Hồ sơ. Chọn xuất bản. Chọn hiển thị đồ thị dạng hình rồi lưu ảnh dạng png
Đúng 0
Bình luận (0)
Cho tam giác ABC có góc A = 60 độ góc B =70 độ
a. Tính góc C .Tam giác ABC là tam giác gì?
b. Vẽ tia Bx //Ac ,tia Cy // AB. Hai tia Bx và Cy cắt nhau tại D .Chứng minh tam giác ABC =tam giác DCB
c. Lấy M là trung điểm BC. chứng minh A,M, D thẳng hàng
10 tháng 12 2021 lúc 8:31
Cho tam giác ABC có AC 5cm, góc A 70°, AB 3 cm. Vẽ AI là tia phângiác góc A (Điểm I thuộc cạnh BC). Vẽ điểm D trên cạnh AC sao cho AD 3 cm.a) Chứng minh: tam giác ABI tam giác ADIb) Gọi H là giao điểm của AI và BD. Chứng minh: HB HDc) Chứng minh: AH vuông góc với BDd) Trên tia AB lấy điểm E sao cho AE 5 cm. Chứng minh: BC DEe) Chứng minh 3 điểm D, I, E thẳng hàng
Đọc tiếp
Cho tam giác ABC có AC= 5cm, góc A = 70°, AB = 3 cm. Vẽ AI là tia phân
giác góc A (Điểm I thuộc cạnh BC). Vẽ điểm D trên cạnh AC sao cho AD = 3 cm.
a) Chứng minh: tam giác ABI = tam giác ADI
b) Gọi H là giao điểm của AI và BD. Chứng minh: HB = HD
c) Chứng minh: AH vuông góc với BD
d) Trên tia AB lấy điểm E sao cho AE = 5 cm. Chứng minh: BC = DE
e) Chứng minh 3 điểm D, I, E thẳng hàng
a: Xét ΔABI và ΔADI có
AB=AD
\(\widehat{BAI}=\widehat{DAI}\)
AI chung
Do đó: ΔABI=ΔADI
Đúng 1
Bình luận (0)