Tìm hàm số bậc 2 biết giá trị nhỏ nhất là 4 khi x=1 và đồ thị qua M(3;0)
Bài 1: Cho hàm số bậc nhất y=(m-1)x+m+3.(d)
a) Vẽ đồ thị hàm số (d) khi m = - 1
b)Tìm giá trị của m để đồ thị của hàm số song song với đồ thị hàm số y = - 2x + 1 .
c) Tìm giá trị của m để đồ thị của hàm số đi qua điểm (1;-4) .
d) Tìm điểm cố định mà đồ thị của hàm số luôn đi qua với mọi m
e) Tìm giá trị của m để đổ thị của hàm số tạo với trục tung và trục hoành một tamgiác có diện tích bằng 1(đvdt ).
c: Thay x=1 và y=-4 vào (d), ta được:
\(m-1+m+3=-4\)
\(\Leftrightarrow2m=-6\)
hay m=-3
Bài 1: Cho hàm số bậc nhất y=(m-1)x+m+3.(d)
a)Tìm giá trị của m để đồ thị của hàm số song song với đồ thị hàm số y = - 2x + 1 .
b) Tìm giá trị của m để đồ thị của hàm số đi qua điểm (1;-4) .
c) Tìm điểm cố định mà đồ thị của hàm số luôn đi qua với mọi m
d) Tìm giá trị của m để đổ thị của hàm số tạo với trục tung và trục hoành một tamgiác có diện tích bằng 1(đvdt ).
Với \(a\ne0\) từ đề bài ta có:
\(\left\{{}\begin{matrix}-\dfrac{b}{2a}=2\\4a+2b+c=1\\16a+4b+c=-3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}4a+b=0\\4a+2b+c=1\\16a+4b+c=-3\end{matrix}\right.\)
\(\Rightarrow a=-1;b=4;c=-3\)
Vậy (P): \(y=-x^2+4x-3\)
1. Xác định hàm số bậc nhất $y = ax + b$ biết rằng đồ thị của hàm số đi qua hai điểm $M(1; -1)$ và $N(2;1)$.
2. Cho phương trình $x^2 - 2mx + m^2 - m + 3 = 0$ (1), trong đó $m$ là tham số.
a. Giải phương trình (1) với $m = 4$.
b. Tìm giá trị của $m$ để phương trình (1) có hai nghiệm $x_1$; $x_2$ và biểu thức $P = x_1 x_2 - x_1 - x_2$ đạt giá trị nhỏ nhất.
1.
Vì đồ thị hàm số đi qua điểm nên
và đi qua điểm nên .
Ta có hệ phương trình .
Vậy hàm số cần tìm là
2.a
Với , phương trình trở thành: .
nên phương trình có hai nghiệm phân biệt và .
2.b.
Ta có .
Phương trình (1) có hai nghiệm , khi
Với , áp dụng định lí Vi-et
Ta có: .
Vì nên suy ra .
Dấu "=" xảy ra khi và chỉ khi
Cho hàm số bậc nhất y=(2m-1)x-2m+5(m là tham số) có đồ thị là đường thẳng (d) và hàm số y=2x+1 có đồ thị là đường thẳng (d')
a. tìm giá trị của m để đường thẳng(d) đi qua điểm A(2;-3)
b. tìm giá trị của m để đường thẳng(d) song song với đường thẳng (d') .với giá trị m vừa tìm được ,vẽ đường thẳng(d) và tính góc α tạo bởi đường thẳng (d) và trục Ox ( làm tròn đến phút)
a: Thay x=2 và y=-3 vào (d), ta được:
\(2\left(2m-1\right)-2m+5=-3\)
=>\(4m-2-2m+5=-3\)
=>2m+3=-3
=>2m=-6
=>\(m=-\dfrac{6}{2}=-3\)
b: Để (d)//(d') thì \(\left\{{}\begin{matrix}2m-1=2\\-2m+5\ne1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2m=3\\-2m\ne-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=\dfrac{3}{2}\\m\ne2\end{matrix}\right.\)
=>m=3/2
Thay m=3/2 vào (d), ta được:
\(y=\left(2\cdot\dfrac{3}{2}-1\right)x-2\cdot\dfrac{3}{2}+5=2x+2\)

y=2x+2 nên a=2
Gọi \(\alpha\) là góc tạo bởi (d) với trục Ox
\(tan\alpha=2\)
=>\(\alpha\simeq63^026'\)
Cho hàm số y = -0,75x2. Qua đồ thị của hàm số đó, hãy cho biết khi x tăng từ -2 đến 4 thì giá trị nhỏ nhất và giá trị lớn nhất của y là bao nhiêu?
- Lập bảng giá trị:
| x | -4 | -2 | 0 | 2 | 4 |
| y = -0,75x2 | -12 | -3 | 0 | -3 | -12 |
- Vẽ đồ thị:
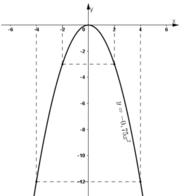
- Quan sát đồ thị hàm số y = -0,75x2:
Khi x tăng từ -2 đến 4, y tăng từ -3 đến 0 rồi lại giảm xuống -12.
Vậy: Giá trị nhỏ nhất của y = -12 đạt được khi x = 4
Giá trị lớn nhất của y = 0 đạt được khi x = 0.
Cho hàm số y = - 0 , 75 x 2 . Qua đồ thị của hàm số đó, hãy cho biết khi x tăng từ -2 đến 4 thì giá trị nhỏ nhất và giá trị lớn nhất của y là bao nhiêu?
- Lập bảng giá trị:
| x | -4 | -2 | 0 | 2 | 4 |
| y = - 0 , 75 x 2 | -12 | -3 | 0 | -3 | -12 |
- Vẽ đồ thị:
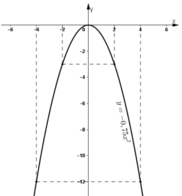
- Quan sát đồ thị hàm số y = - 0 , 75 x 2 :
Khi x tăng từ -2 đến 4, y tăng từ -3 đến 0 rồi lại giảm xuống -12.
Vậy: Giá trị nhỏ nhất của y = -12 đạt được khi x = 4
Giá trị lớn nhất của y = 0 đạt được khi x = 0.
Cho hàm số f(x) có đạo hàm là hàm f'(x). Đồ thị hàm số f'(x) như hình vẽ bên. Biết rằng f(0) + f(1) - 2f(2) = f(4) - f(3). Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của f(x) trên đoạn [0;4].

A. m = f(4), M = f(2)
B. m = f(1), M = f(2)
C. m = f(4), M = f(1)
D. m = f(0), M = f(2)
Chọn A
Dựa vào đồ thị của hàm f'(x) ta có bảng biến thiên.
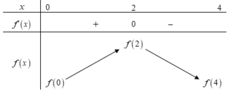
Vậy giá trị lớn nhất M = f(2)
Hàm số đồng biến trên khoảng (0;2) nên f(2) > f(1) => f(2) - f(1) > 0 .
Hàm số nghịch biến trên khoảng (2;4) nên f(2) > f(3) => f(2) - f(3) > 0.
Theo giả thuyết: f(0) + f(1) - 2f(2) = f(4) - f(3).
![]()
=> f(0) > f(4)
Vậy giá trị nhỏ nhất m = f(4)
cho hàm số bậc nhất y=(m-2)x+m+1 ( với m là tham số m khác 2 ) a) tìm các giá trị của m để đồ thi hàm số đã cho đi qua A(1;-1) b) tìm các giá trị của m đẻ đồ thị của m để đồ thị hàm số đã cắt cho đường thẳng y=x+2 tại 1 điểm trên trục hoành
a: Thay x=1 và y=-1 vào (d), ta được:
\(\left(m-2\right)\cdot1+m+1=-1\)
=>m-2+m+1=-1
=>2m-1=-1
=>2m=0
=>m=0
b: Thay y=0 vào y=x+2, ta được:
x+2=0
=>x=-2
Thay x=-2 và y=0 vào y=(m-2)x+m+1, ta được:
-2(m-2)+m+1=0
=>-2m+4+m+1=0
=>5-m=0
=>m=5