Tìm a, b để:
2x3-x2+ab+b chia hết x2-1
Tìm a, b để đa thức A ( x ) = 2 x 3 – x 2 + a x + b chia hết cho đa thức B ( x ) = x 2 – 1
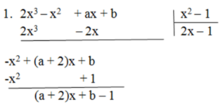
A(x) chia hết cho B(x) khi (a + 2)x + b – 1 là đa thức 0
Vậy a + 2 = 0 và b – 1 = 0 ⇒ a = -2 và b = 1
Tìm a, b để đa thức A ( x ) = 2 x 3 – x 2 + a x + b chia hết cho đa thức B ( x ) = x 2 – 1
Tìm a, b để đa thức A ( x ) = 2 x 3 – x 2 + a x + b chia hết cho đa thức B ( x ) = x 2 – 1
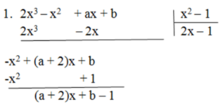
A(x) chia hết cho B(x) khi (a + 2)x + b – 1 là đa thức 0
Vậy a + 2 = 0 và b – 1 = 0 ⇒ a = -2 và b = 1
tìm a b để f(x)=3x4-2x3+(a-1)x2+3x+b chia hết cho g(x)=x2-3x+2
Lời giải:
Ta thấy: $x^2-3x+2=(x-1)(x-2)$. Do đó để $f(x)$ chia hết cho $g(x)$ thì $f(x)\vdots x-1$ và $f(x)\vdots x-2$
Tức là $f(1)=f(2)=0$ (theo định lý Bê-du)
$\Leftrightarrow 3-2+(a-1)+3+b=3.2^4-2.2^3+(a-1).2^2+3.2+b=0$
$\Leftrightarrow a+b=-3$ và $4a+b=-34$
$\Rightarrow a=\frac{-31}{3}$ và $b=\frac{22}{3}$
Tìm a, b để đa thức A ( x ) = 2 x 3 + 7 x 2 + a x + b chia hết cho đa thức B ( x ) = x 2 + x – 1
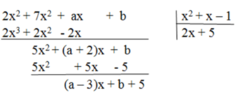
A(x) chia hết cho B(x) khi (a – 3)x + b + 5 là đa thức 0
⇒ a – 3 = 0 hoặc b + 5 = 0 ⇒ a = 3 hoặc b = -5
Tìm a để đa thức A chia hết cho đa thức B với:
A = 2 x 3 - 7 x 2 - 11x + a - 8 và B = 2 x 2 + 3x + 4.
Thực hiện chia đa thức A cho B được đa hức dư là a + 12
Từ A chia hết cho B Þ a + 12 = 0 Û a = -12.
tìm x nguyên để giá trị của đa thức A chia hết cho giá trị của đa thức B.
a) A = -2x3-3x2+12x+2 và B =2x-1
b) A =-3x3+x2+15x-6 và B =3x+1
Tìm x nguyên để các phép chia sau là phép chia hết: ( mình cần gấp
(2x3-x2+4) : (x+1)
Lời giải:
$2x^3-x^2+4=2x^2(x+1)-3x(x+1)+3(x+1)+1$
$=(x+1)(2x^2-3x+3)+1$
Với $x$ nguyên, để $2x^3-x^2+4\vdots x+1$ thì $1\vdots x+1$
$\Rightarrow x+1\in \text{Ư(1)}$
$\Rightarrow x+1\in\left\{\pm 1\right\}$
$\Rightarrow x\in\left\{-2; 0\right\}$
Có bao nhiêu số nguyên x để giá trị của đa thức A = 2 x 3 – 3 x 2 + 2x + 2 chia hết cho giá trị của đa thức B = x 2 + 1
A. 3
B. 4
C. 2
D. 1
Ta có A : B

Để giá trị của đa thức A = 2 x 3 – 3 x 2 + 2x + 2 chia hết cho giá trị của đa thức B = x 2 + 1 thì
5 ⁝ ( x 2 + 1)
Hay ( x 2 + 1) Є U(5) = {-1; 1; -5; 5}
+) x 2 + 1 = -1 ó x 2 = -2 (VL)
+) x 2 + 1 = 1 ó x 2 = 0ó x = 0 (tm)
+) x 2 + 1 = -5 ó x 2 = -6 (VL)
+) x 2 + 1 = 5 ó x 2 = 4 ó x = ± 2 ™
Vậy có 3 giá trị của x thỏa mãn đề bài là x = 0; x = -2; x = 2
Đáp án cần chọn là: A
Bài 5: Tìm a, b sao cho
a/ Đa thức x4 – x3 + 6x2 – x + a chia hết cho đa thức x2 – x + 5
b/ Đa thức 2x3 – 3x2 + x + a chia hết cho đa thức x + 2.
Đặt \(f\left(x\right)=2x^3-3x^2+x+a\)
Ta có: phép chia \(f\left(x\right)\) cho \(x+2\) có dư là \(R=f\left(-2\right)\)
\(\Rightarrow f\left(-2\right)=2.\left(-2\right)^3-3.\left(-2\right)^2+\left(-2\right)+a\)
\(f\left(-2\right)=2.\left(-8\right)-3.4-2+a\)
\(f\left(-2\right)=-16-12-2+a\)
\(f\left(-2\right)=-20+a\)
Để \(f\left(x\right)\) chia hết cho \(x+2\) thì \(R=0\) hay \(f\left(-2\right)=0\)
\(\Rightarrow-20+a=0\Leftrightarrow a=20\)