Tìm x ạ, cái dấu đó là giá trị tuyệt đối nha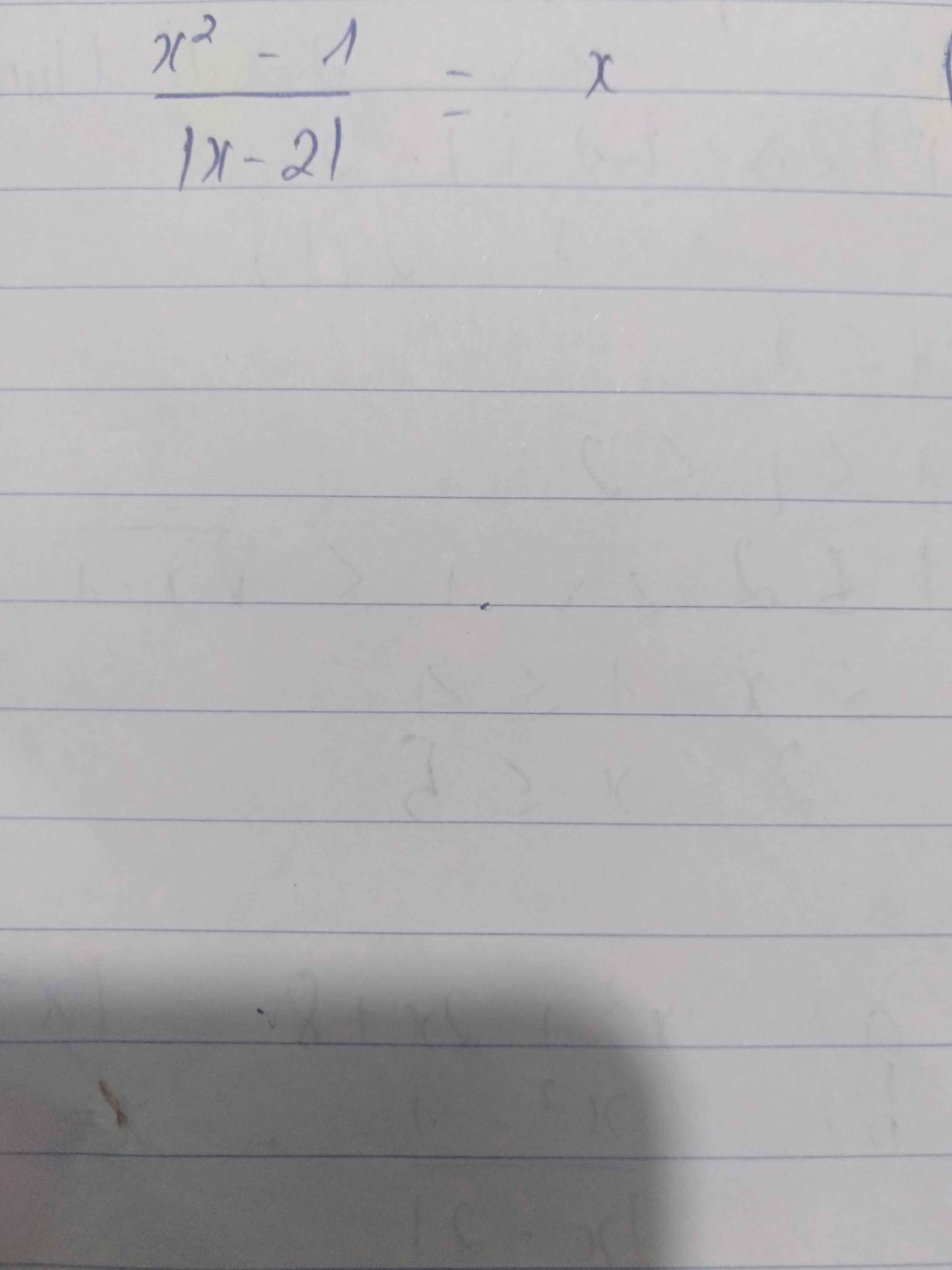

Những câu hỏi liên quan
Tim x, biết :
a) /x-2/=x
b) /x-3,4/+/2.6-x/=0
(Cái dấu đó là giá trị tuyệt đối nha mấy bn)
a.\(\left|x-2\right|=x\)
\(\orbr{\begin{cases}x-2=x\\x-2=-x\end{cases}\Rightarrow\orbr{\begin{cases}-2=x-x\\-2=-x-x\end{cases}}}\Rightarrow\orbr{\begin{cases}-2=0\left(KTM\right)\\-2=-2x\end{cases}}\Rightarrow x=1\)
b. \(\left|x-3,4\right|+\left|2,6-x\right|=0\)
\(\hept{\begin{cases}\left|x-3,4\right|=0\\\\\left|2,6-x\right|=0\end{cases}}\Rightarrow\hept{\begin{cases}x-3,4=0\\\\2,6-x=0\end{cases}}\Rightarrow\hept{\begin{cases}x=3,4\\\\x=2,6\end{cases}}\)
Cố gắng học tốt nhé bạn !!!
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất của các biểu thứca) A / x-1/+2018b) B/ x+2 /+ / y-1/ + 10c) C ^{left(x+1right)^2} + /y-5 /LƯU Ý: Cái / là do mk k biết viết dấu giá trị tuyệt đối ạ. mk viết / là thay cho dấu của giá trị tuyệt đối nhaCác bạn làm sớm và giúp mk với ạ. ai nhanh mà giải đúng là mk sẽ tick cho bạn ấy nhaCảm ơn nhiều ạ
Đọc tiếp
Tìm giá trị nhỏ nhất của các biểu thức
a) A= / x-1/+2018
b) B=/ x+2 /+ / y-1/ + 10
c) C= \(^{\left(x+1\right)^2}\) + /y-5 /
LƯU Ý: Cái ''/'' là do mk k biết viết dấu giá trị tuyệt đối ạ. mk viết ''/'' là thay cho dấu của giá trị tuyệt đối nha
Các bạn làm sớm và giúp mk với ạ. ai nhanh mà giải đúng là mk sẽ tick cho bạn ấy nha
Cảm ơn nhiều ạ
\(A=\left|x-1\right|+2018\)
ta có :
\(\left|x-1\right|\ge0\)
\(\Rightarrow\left|x-1\right|+2018\ge0+2018\)
\(\Rightarrow\left|x-1\right|+2018\ge2018\)
dấu "=" xảy ra khi :
\(\left|x-1\right|=0\)
\(\Rightarrow x-1=0\)
\(\Rightarrow x=1\)
vậy MinA = 2018 khi x = 1
Đúng 0
Bình luận (0)
Bạn nào thông minh giải cả 3 câu hộ mình luôn nha. mk đang cần gấp các bạn ơi
Đúng 0
Bình luận (0)
\(B=\left|x+2\right|+\left|y-1\right|+10\)
Ta có: \(\hept{\begin{cases}\left|x+2\right|\ge0\forall x\\\left|y-1\right|\ge0\forall y\end{cases}\Rightarrow\left|x+2\right|+\left|y-1\right|+10\ge10\forall x}\)
\(B=10\Leftrightarrow\hept{\begin{cases}\left|x+2\right|=0\\\left|y-1\right|=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=-2\\y=1\end{cases}}}\)
Vậy \(B_{min}=10\Leftrightarrow\hept{\begin{cases}x=-2\\y=1\end{cases}}\)
\(C=\left(x+1\right)^2+\left|y-5\right|\)
Ta có: \(\hept{\begin{cases}\left(x+1\right)^2\ge0\forall x\\\left|y-5\right|\ge0\forall y\end{cases}}\Rightarrow\left(x+1\right)^2+\left|y-5\right|\ge0\forall x;y\)
\(C=0\Leftrightarrow\hept{\begin{cases}\left(x+1\right)^2=0\\\left|y-5\right|=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=-1\\y=5\end{cases}}}\)
Vậy \(C_{min}=0\Leftrightarrow\hept{\begin{cases}x=-1\\y=5\end{cases}}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tìm số nguyên x biết
/x-2/-x =4 (dấu / là dấu giá trị tuyệt đối nha)
tìm x:
/x-1/+/x-3/=2
dấu / là dấu giá trị tuyệt đối nha
* Nếu \(x< 1\)
=> 1 - x + 3 - x = 2
<=> 4 - 2x = 2
<=> x = 1 (không TM)
* Nếu \(1\le x< 3\)
=> x - 1 + 3 - x = 2
<=> 2 = 2 (đúng)
=> phương trình luôn có nghiệm.
* Nếu \(x\ge3\)
=> x - 1 + x - 3 = 2
<=> 2x - 4 = 2
<=> x = 3 (TM)
Vậy với \(1\le x< 3\)thì phương trình luôn có nghiệm
với \(x\ge3\)thì phương trình có nghiệm x = 3.
Đúng 0
Bình luận (0)
Ta có \(|x-1|+|x-3|=2\)\(\Rightarrow|x-1|+|3-x|=2\)
Áp dụng bất đẳng thức \(|a|+|b|\ge|a+b|\)
Dấu bằng xảy ra khi và chỉ khi \(ab\ge0\)
Do đó \(|x-1|+|3-x|\ge|x-1+3-x|=|2|=2\)
Dấu bằng xảy ra khi và chỉ khi \(\left(x-1\right)\left(3-x\right)\ge0\)
\(\cdot\orbr{\begin{cases}\hept{\begin{cases}x-1\ge0\\3-x\ge0\end{cases}}\\\hept{\begin{cases}x-1\le0\\3-x\le0\end{cases}}\end{cases}}\)\(\Rightarrow\hept{\begin{cases}x-1\ge0\\3-x\ge0\end{cases}}\)hoặc \(\hept{\begin{cases}x-1\le0\\3-x\le0\end{cases}}\)
\(\cdot\hept{\begin{cases}x-1\ge0\\3-x\ge0\end{cases}}\Rightarrow\hept{\begin{cases}x\ge1\\x\le3\end{cases}}\Rightarrow1\le x\le3\)
\(\cdot\hept{\begin{cases}x-1\le0\\3-x\le0\end{cases}}\Rightarrow\hept{\begin{cases}x\le1\\x\ge3\end{cases}}\)( vô lý )
Vậy \(1\le x\le3\)
PS : vì đề bài không yêu cầu tìm \(x\in Z\) nên mình để đáp số như vậy
còn nếu yêu cầu bạn phải tìm được 3 giá trị của x là 1;2;3
Đúng 0
Bình luận (0)
TH1: \(x\le1\)
pt <=> 1-x+3-x=2 <=> 4-2x=2 <=> 2x=2 <=> x=1 (loại)
TH2: \(1\le x\le3\)
pt <=> x-1+3-x=2 <=> 2=2 luôn đúng
TH3: x>3
pt <=> x-1+x-3=2 <=> 2x-4=2 <=> 2x=6 <=> x=3 (loại)
Vậy \(1\le x\le3\)
Đúng 0
Bình luận (0)
Tìm x biết:/2x+1/=/x-3/=5
dấu // là giá trị tuyệt đối của mik nha ai làm đầu tiên mik sẽ tích cho người đó nha!!!!!!!
/x-1,3/+/2x-1/=0
tìm x
(lưu ý dấu " / "này là dấu giá trị tuyệt đối nha!)
|x - 1,3| + |2x - 1| = 0
Có |x - 1,3| \(\ge\)0
|2x - 1| \(\ge\)0
=> Để |x - 1,3| + |2x - 1| = 0
=> |x - 1,3| = 0 và |2x - 1| = 0
=> x - 1,3 = 0 và 2x - 1 = 0
=> x = 1,3 và 2x = 1
=> x = 1,3 và x = 0,5 (vô lí vì x không thể cùng lúc nhận 2 giá trị)
=> Không có giá trị của x thỏa mãn đề bài
Đúng 0
Bình luận (0)
Tìm x,y để C= -18-[2x-6]-[3y+9] đạt giá trị lớn nhất
Hai dấu "[" và "]" là dấu giá trị tuyệt đối nha
nếu cậu muốn giá trị tuyệt đối thay vì cái dấu ngoặc vuông ấy thì chỉ cần bấm và giữ shift với phím bên trái của phím end là ra giá trị tuyệt đối thôi
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Các bạn chỉ mình : Ví dụ căn 45a . Căn 4a -5a chẳng hạn khi mà a <0 thì chỉ đổi dấu ở chỗ giá trị tuyệt đối thôi ạ còn cái a mà ko nằm trong trị tuyệt đối thì không đỏi dấu ạ
Tìm gia trị lớn nhất của biểu thức
B=/x-7/+/y-5/+1890
Cái dấu "/ /"là giá trị tuyệt đối nhaa























