Cho tam giác ABC các đường cao AD,BE,CF cắt nhau tại H. Chỉ ra tất cả các tứ giác nội tiếp.

Những câu hỏi liên quan
Cho tam giác ABC nhọn, các đường cao AD, BE, CF cắt nhau tại H
a)Chứng minh tứ giác BFHD, BFEC nội tiếp
b) Chỉ ra các tứ giác còn lại nội tiếp được đường tròn
c) Chứng minh H là tâm của đường tròn nội tiếp tam giác EFD
d) Gọi M là trung điểm của BC. Chứng minh tứ giác EFDM nội tiếp
Xem chi tiết
a) Xét tứ giác BFHD có
\(\widehat{BFH}\) và \(\widehat{BDH}\) là hai góc đối
\(\widehat{BFH}+\widehat{BDH}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: BFHD là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Xét tứ giác BFEC có
\(\widehat{BFC}=\widehat{BEC}\left(=90^0\right)\)
\(\widehat{BFC}\) và \(\widehat{BEC}\) cùng nhìn cạnh BC một góc bằng 900
Do đó: BFEC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Đúng 5
Bình luận (0)
Cho tam giác ABC nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại H. Các tứ giác nào sau đây nội tiếp được đường tròn.
A.AEHF
B. BFEC
C. AEDB
D. Cả A, B, C.
▲ABC, đường cao AD, BE, CF. Chỉ ra tất cả các tứ giác nội tiếp
bài tập 1: cho tam giác abc có các đường cao ad, be, cf cắt nhau tại h. chứng minh rằng các tứ giác aehf, cdhf, behd nội tiếp.
Câu 5 (3,0 điểm). Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn tâm O. Các đường cao
AD, BE, CF của tam giác ABC cắt nhau tại H.
a) Chứng minh các tứ giác AEHF, BFEC nội tiếp đường tròn.
b) Đường thẳng AO cắt đường tròn tâm O tại điểm K khác điểm A. Gọi I là giao điểm của
hai đường thẳng HK và BC. Chứng minh I là trung điểm của đoạn thẳng BC.
c, tinh AH/AD + BH/BE + CH/CF 2
Đọc tiếp
Câu 5 (3,0 điểm). Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn tâm O. Các đường cao
AD, BE, CF của tam giác ABC cắt nhau tại H.
a) Chứng minh các tứ giác AEHF, BFEC nội tiếp đường tròn.
b) Đường thẳng AO cắt đường tròn tâm O tại điểm K khác điểm A. Gọi I là giao điểm của
hai đường thẳng HK và BC. Chứng minh I là trung điểm của đoạn thẳng BC.
c, tinh AH/AD + BH/BE + CH/CF =2
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn(O).
Các đường cao AD, BE, CF cắt nhau tại H và cắt đường tròn (O) lần lượt tại M, N, P. CMR:
a/. Các tứ giác AEHF, BCEF nội tiếp
b/ AD.BC = BE AC
c/. CMR BHM cân
Cho tam giác ABC nội tiếp đường tròn (O), các đường cao AD, BE, CF cắt nhau tại H và lần lượt cắt đường tròn tại M, N, P. Chứng minh rằng:
1) Tứ giác BFEC và AEDB nội tiếp.
2) AE.AC = AF.AB.
3) Chứng minh H là tâm đường tròn nội tiếp tam giác EFD.
1: Xét tứ giác BFEC có
\(\widehat{BFC}=\widehat{BEC}=90^0\)
Do đó: BFEC là tứ giác nội tiếp
Xét tứ giác AEDB có
\(\widehat{AEB}=\widehat{ADB}=90^0\)
Do đó: AEDB là tứ giác nội tiếp
2: Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
\(\widehat{EAB}\) chung
Do đó: ΔAEB\(\sim\)ΔAFC
Suy ra: AE/AF=AB/AC
hay \(AE\cdot AC=AB\cdot AF\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn tâm O. Các đường cao AD,BE,CF cắt nhau tại H. Vẽ tiếp tuyến của đường tròn O tại A. Đường thẳng EF cắt đường tròn O tại I Và K a) CM: các tứ giác BFHD,BFEC nội tiếp b) CM:EB là tia phân giác của góc FED c)CM: OA vuông góc IK d) gọi S là tâm đường tròn ngoại tiếp tam giác BCE,đường thẳng vuô g góc với HS tại S cắt AB tại P, cắt AC tạ...
Đọc tiếp
Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn tâm O. Các đường cao AD,BE,CF cắt nhau tại H. Vẽ tiếp tuyến của đường tròn O tại A. Đường thẳng EF cắt đường tròn O tại I Và K a) CM: các tứ giác BFHD,BFEC nội tiếp b) CM:EB là tia phân giác của góc FED c)CM: OA vuông góc IK d) gọi S là tâm đường tròn ngoại tiếp tam giác BCE,đường thẳng vuô g góc với HS tại S cắt AB tại P, cắt AC tại Q và cắt AD tại G. Chứng minh PG=GQ
a: góc BDH+góc BFH=180 độ
=>BDHF nội tiếp
góc BFC=góc BEC=90 dộ
=>BFEC nội tiếp
b: góc FEB=góc BAD
góc DEB=góc FCB
mà góc BAD=góc FCB
nên góc FEB=góc DEB
=>EB là phân giác của góc FED
c: Kẻ tiếp tuyến Ax của (O)
=>góc xAC=góc ABC=góc AEF
=>Ax//FE
=>FE vuông góc OA
=>OA vuông góc IK
Đúng 1
Bình luận (0)
Cho tam giác ABC nhọn nội tiếp (O) . Các đường cao AD, BE , và CF cắt nhau tại H . Đường thẳng EF cắt đường tròn ở I và K a) chứng minh : Tứ giác CDHE nội tiếp đường trònb) Chứng minh : AH . AD = AF . ABc) Kẻ tiếp tuyến Ax, chứng minh: BCEF nội tiếp. Từ đó chứng minh : Ax // IK
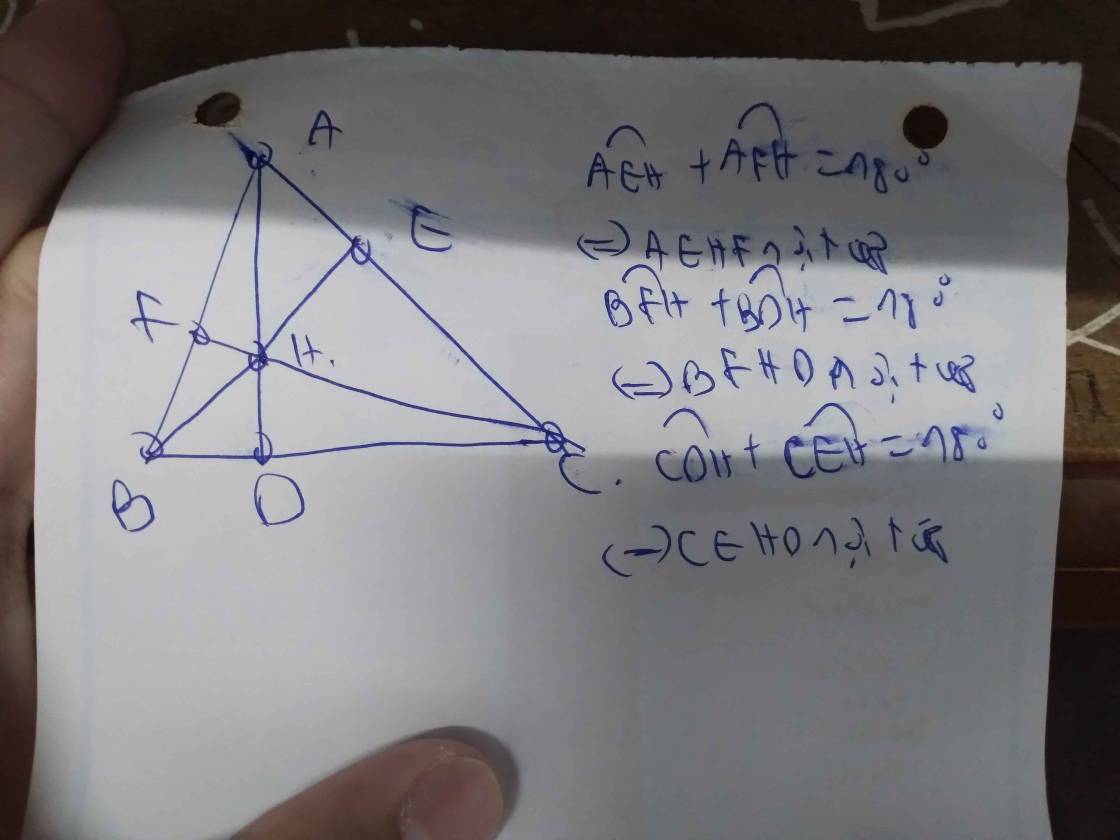
 h vẽ như sau:
h vẽ như sau:
Xét tứ giác CEHD ta có:
Góc CEH = 900 (Vì BE là đường cao)
Góc CDH = 900 (Vì AD là đường cao)
=> góc CEH + góc CDH = 1800
Mà góc CEH và góc CDH là hai góc đối của tứ giác CEHD. Do đó CEHD là tứ giác nội tiếp
Đúng 1
Bình luận (0)