cho hàm số y = f(x) = \(2\sin2x\) .
a) lập bảng biến thiên của hàm số y = \(2\sin2x\) trên đoạn \(\left[-\frac{\pi}{2};\frac{\pi}{2}\right]\)
b) vẽ đồ thị của hàm số y = \(2\sin2x\) .
Cho hàm số y = f(x). Hàm số y = f’(x) có bảng biến thiên như hình vẽ bên. Giá trị lớn nhất của hàm số g x = f 2 x - sin 2 x trên đoạn [-1;1]?
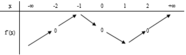
A. f(-1)
B. f(0)
C. f(2)
D. f(1)
cho hàm số y = f(x) = \(2\sin2x\) .
a) lập bảng biến thiên của hàm số y = \(2\sin2x\) trên đoạn \(\left[-\frac{\pi}{2};\frac{\pi}{2}\right]\)
b) vẽ đồ thị của hàm số y = \(2\sin2x\) .
cho hàm số y = f(x) = \(2\sin2x\) .
a) lập bảng biến thiên của hàm số y = \(2\sin2x\) trên đoạn \(\left[-\frac{\pi}{2};\frac{\pi}{2}\right]\)
b) vẽ đồ thị của hàm số y = \(2\sin2x\) .
Cho hàm số y=f(x). Hàm số y=f '(x) có bảng biến thiên như hình vẽ dưới
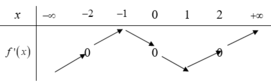
Giá trị lớn nhất của hàm số g ( x ) = f ( 2 x ) - sin 2 x trên [-1;1]
A. f(-1)
B. f(0)
C. f(2)
D. f(1)
Ta có g ( x ) = f ( 2 x ) - sin 2 x ≤ f ( 2 x ) 2 x ∈ - 2 ; 2 suy ra bảng biến thiên
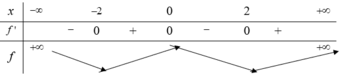
Dựa vào BBT suy ra f ( 2 x ) ≤ f ( 0 ) ⇒ g ( x ) ≤ f ( 0 ) ∀ 2 x ∈ - 2 ; 2
⇒ m a x [ - 1 ; 1 ] g ( x ) = f ( 0 ) đạt được khi
x = 0 sin 2 x = 0 ⇔ x = 0
Chọn đáp án B.
Cho hàm số y = f x . Hàm số y = f ' x có bảng biến thiên như hình vẽ dưới
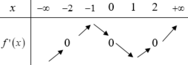
Giá trị lớn nhất của hàm số g x = f 2 x - sin 2 x trên [ -1;1]
A. f - 1
B. f 0
C. f 2
D. f 1
Xét tính tăng giảm và lập bảng biến thiên của hàm số y = sin2x trên \(\left[-\dfrac{\pi}{2};\dfrac{\pi}{2}\right]\)
\(y'=-2cos2x=0\Rightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{4}\\x=\dfrac{\pi}{4}\end{matrix}\right.\)
BBT:
Hàm đồng biến trên \(\left(-\dfrac{\pi}{4};\dfrac{\pi}{4}\right)\) và nghịch biến trên các khoảng \(\left(-\dfrac{\pi}{2};-\dfrac{\pi}{4}\right);\left(\dfrac{\pi}{4};\dfrac{\pi}{2}\right)\)
Cho hàm số y=f(x) = 4x^2+ 6x-5 a) Lập bảng biến thiên và vẽ đồ thị hàm số y= f(×). b) Từ bảng biến thiên, xác định khoảng đồng biến và nghịch biến và giá trị nhỏ nhất của hàm số trên c) Từ bảng biến thiên tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số trên đoạn [-1;2]
a: Tọa độ đỉnh là:
\(\left\{{}\begin{matrix}x=\dfrac{-6}{2\cdot4}=\dfrac{-6}{8}=\dfrac{-3}{4}\\y=-\dfrac{6^2-4\cdot4\cdot\left(-5\right)}{4\cdot4}=-\dfrac{29}{4}\end{matrix}\right.\)
Bảng biến thiên là:
| x | -\(\infty\) -3/4 +\(\infty\) |
| y | -\(\infty\) -29/4 +\(\infty\) |
b: Hàm số đồng biến khi x>-3/4; nghịch biến khi x<-3/4
GTNN của hàm số là y=-29/4 khi x=-3/4
Cho hàm số y=f(x)= -3x^2+10x-4 a) Lập bảng biến thiên và vẽ đồ thị hàm số y= f(×) b) Từ bảng biến thiên, xác định khoảng đồng biến và nghịch biến và giá trị nhỏ nhất của hàm số trên c) Từ bảng biến thiên tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số trên đoạn [-1;2]
a: Tọa độ đỉnh là:
\(\left\{{}\begin{matrix}x=\dfrac{-10}{2\cdot\left(-3\right)}=\dfrac{10}{6}=\dfrac{5}{3}\\y=-\dfrac{10^2-4\cdot\left(-3\right)\cdot\left(-4\right)}{4\cdot\left(-3\right)}=\dfrac{13}{3}\end{matrix}\right.\)
Bảng biến thiên:
| x | -\(\infty\) 5/3 +\(\infty\) |
| y | +\(\infty\) 13/3 -\(\infty\) |
b: Hàm số đồng biến khi x<5/3; nghịch biến khi x>5/3
Giá trị nhỏ nhất là y=13/3 khi x=5/3
