Có bao nhiêu số tự nhiên gồm 4 chữ số khác nhau được lấy từ tập E= {0;1;2;3;4;5;6;7} sao cho tổng các chữ số trong mỗi số : a) là 1 số lẻ b) là 1 số chẵn.

Những câu hỏi liên quan
Cho tập hợp S = 1 ; 2 ; 3 ; 4 ; 5 ; 6 . Có thể lập được bao nhiêu số tự nhiên gồm 4 chữ số khác nhau lấy từ tập hợp S?
A. 360
B. 120
C. 15
D. 20
Chọn đáp án A.
Cách 1: Lấy 4 chữ số khác nhau từ tập S rồi sắp xếp theo một thứ tự nào đó ta được một số tự nhiên.
Vậy số tự nhiên gồm 4 chữ số khác nhau lấy từ tập hợp S là một chỉnh hợp chập 4 của S.
Do đó số các số tự nhiên gồm 4 chữ số khác nhau lấy từ tập hợp S là A 6 4 = 360 (số).
Cách 2: Có 6 cách chọn chữ số hàng nghìn.
Khi đó có 5 cách chọn chữ số hàng trăm.
Khi đã chọn xong chữ số hàng nghìn và chữ số hàng tram thì có 44 cách chọn chữ số hàng chục
Cuốin ùng, khi đã chọn xong chữ số hang nghìn, hằng trăm, hàng chục thì còn 3 cách chọn chữ số hàng đơn vị.
Vậy các số tự nhiên gồm 4 chữ số khác nhau lấy từ tập hợp S là 6.5.4.3 = 360 (số).
Đúng 0
Bình luận (0)
Có bao nhiêu số tự nhiên gồm 4 chữ số khác nhau được lấy từ tập E= {0;1;2;3;4;5;6;7} sao cho tổng các chữ số trong mỗi số : a) là 1 số lẻ b) là 1 số chẵn.
1. Gọi S là tập hợp tất cả các số tự nhiên gồm 4 chữ số khác nhau được chọn từ các chữ số từ 1 đến 7 chọn ngẫu nhiên 1 số từ S tính xác suất để số được chọn là số lẻ và có mặt chữ số 5.2. Tập hợp E gồm các chữ số từ 1 đến 5. Gọi M là tập hợp tatts cả các số tự nhiên có ít nhất 3 chữ số đôi 1 khác nhau. Lấy 1 số từ M tính xác suất để tổng các chữ số của số đó bằng 10.3. Từ các chữ số 0,1,2,3,4,5,6,7 có thể lập được bao nhiêu số tự nhiên gồm 5 chữ số khác nhautrong đó có đúng 2 chữ số chẵn
Đọc tiếp
1. Gọi S là tập hợp tất cả các số tự nhiên gồm 4 chữ số khác nhau được chọn từ các chữ số từ 1 đến 7 chọn ngẫu nhiên 1 số từ S tính xác suất để số được chọn là số lẻ và có mặt chữ số 5.
2. Tập hợp E gồm các chữ số từ 1 đến 5. Gọi M là tập hợp tatts cả các số tự nhiên có ít nhất 3 chữ số đôi 1 khác nhau. Lấy 1 số từ M tính xác suất để tổng các chữ số của số đó bằng 10.
3. Từ các chữ số 0,1,2,3,4,5,6,7 có thể lập được bao nhiêu số tự nhiên gồm 5 chữ số khác nhautrong đó có đúng 2 chữ số chẵn
Câu 1: Từ các số 1; 2; 3; 4; 5; 6; 7. Có thể lập được bao nhiêu số tự nhiên lẻ có 5 chữ số đôi một khác nhau.
Câu 2: Cho tập A gồm các số 0; 1; 2; 3; 4; 5.
a) Có bao nhiêu số tự nhiên có 4 chữ số khác nhau?
b) Chọn ngẫu nhiên 1 số tự nhiên từ các số thành lập ở trên. Tính xác suất để chọn được số chẵn.
1.
Chữ số hàng đơn vị có 4 cách chọn (từ 1,3,5,7)
Chọn và hoán vị 4 chữ số từ 6 chữ số còn lại: \(A_6^4\) cách
Tổng cộng: \(4.A_6^4\) cách
2.
Gọi chữ số cần lập có dạng \(\overline{abcd}\)
a.
Lập số có 4 chữ số bất kì (các chữ số đôi một khác nhau): \(A_6^4\) cách
Lập số có 4 chữ số sao cho số 0 đứng đầu: \(A_5^3\) cách
\(\Rightarrow A_6^4-A_5^3=300\) số
b.
Để số được lập là số chẵn \(\Rightarrow\) d chẵn
TH1: \(d=0\Rightarrow abc\) có \(A_5^3\) cách chọn
TH2: \(d\ne0\Rightarrow d\) có 2 cách chọn (từ 2;4)
a có 4 cách chọn (khác 0 và d), b có 4 cách chọn, c có 3 cách chọn
\(\Rightarrow2.4.4.3=96\) số
Tổng cộng: \(A_5^3+96=156\) số
Xác suất \(P=\dfrac{156}{300}=...\)
Đúng 1
Bình luận (2)
Cho tập A = {0,1,2,3,4,5}. Có bao nhiêu số tự nhiên chẵn gồm 4 chữ số đôi một khác nhau chia hết cho 10 lấy từ tập A
Có \(A^3_5=60\) số tự nhiên thỏa mãn yêu cầu bài toán.
Đúng 1
Bình luận (0)
Từ các số: 0;1;2;3;4;5a) Hỏi có thể lập được bao nhiêu số tự nhiên gồm 4 chữ sốb) Hỏi có thể lập được bao nhiêu số tự nhiên gồm 4 chữ số đôi một khác nhauc) Hỏi có thể lập được bao nhiêu số tự nhiên gồm 4 chữ số khác nhau và là số chẵnd) Hỏi có thể lập được bao nhiêu số tự nhiên gồm 4 chữ số khác nhau chia hết cho 5e) Hỏi có thể lập được bao nhiêu số tự nhiên gồm 4 chữ số có đôi một khác nhau 3000
Đọc tiếp
Từ các số: 0;1;2;3;4;5
a) Hỏi có thể lập được bao nhiêu số tự nhiên gồm 4 chữ số
b) Hỏi có thể lập được bao nhiêu số tự nhiên gồm 4 chữ số đôi một khác nhau
c) Hỏi có thể lập được bao nhiêu số tự nhiên gồm 4 chữ số khác nhau và là số chẵn
d) Hỏi có thể lập được bao nhiêu số tự nhiên gồm 4 chữ số khác nhau chia hết cho 5
e) Hỏi có thể lập được bao nhiêu số tự nhiên gồm 4 chữ số có đôi một khác nhau <3000
Số cách chọn : \(5\times6\times6\times6=1080\)(vì chỉ có 5 cách chọn số đứng đầu)
b) số cách lập số tự nhiên có 4 chữ số :
-Có 5 cách chọn chữ số làm số đầu (1;2;3;4;5) vì số 0 không đứng đầu được
-Có 5 cách chon số thứ hai vì đã chọn 1 số đứng đầu
-Có 4 cách chọn số thứ ba vì đã chọn hai số đầu
-có 3 cách chon số thứ 4 vì chọn 3 số đầu
Suy ra có số cách chọn : \(5\times5\times4\times3=300\)
Đúng 2
Bình luận (0)
Cho tập hợp A ={0, 1,2,3,4,5,6}. Từ tập A lập được bao nhiêu số tự nhiên chẵn gồm bốn chữ số khác nhau mà trong đó có chữ số 2 ?
Xem chi tiết
giúp mình với
Gọi số tự nhiên gồm 4 chữ số là: abcd
Trường hợp 1: d=0 (1 cách)
a : 6 cách ( #0); b: 5 cách; c:4 cách => 120 cách
TH2: d#0 ( nhận 2 4 6 => 1 cách)
a: 5 cách (#0; #d); b : 4 cách; c: 3 cách => 60 cách
=> TH1 + TH2 = 200 cách
Đúng 0
Bình luận (0)
ý lộn TH2: b: 5 cách(#a; #d); c: 4 cách => 100 cách
=> Tổng cộng 220 cách
Đúng 0
Bình luận (0)
Gọi A là tập các số tự nhiên gồm 5 chữ số mà các chữ số đều khác 0. Lấy ngẫu nhiên từ tập A một số. Tính xác suất để lấy được số mà chỉ có đúng 3 chữ số khác nhau.
A
.
1400
19683
B
.
560
6561
C
.
1400
6561
D
.
2240
6561
Đọc tiếp
Gọi A là tập các số tự nhiên gồm 5 chữ số mà các chữ số đều khác 0. Lấy ngẫu nhiên từ tập A một số. Tính xác suất để lấy được số mà chỉ có đúng 3 chữ số khác nhau.
A . 1400 19683
B . 560 6561
C . 1400 6561
D . 2240 6561
Chọn C
Gọi x là số bi của hộp thứ nhất nên số bi ở hộp thứ hai là 20 - x ![]() )
)
Gọi a,b ![]() lần lượt là số bi xanh hộp thứ nhất và số bi xanh ở hộp thứ hai.
lần lượt là số bi xanh hộp thứ nhất và số bi xanh ở hộp thứ hai.
Suy ra: 0 < a < x, 0 < b < 20 - x
Số cách lấy bi ở mỗi hộp là độc lập với nhau nên ta đặt:
+) Xác suất lấy một bi xanh ở hộp thứ nhất là a x và ở hộp thứ hai là b 20 - x
Với a, b, x là các số tự nhiên thỏa mãn ![]()
+) Xác suất lấy được hai bi xanh 
Ta có ![]()
![]()
Lập bảng thử từng giá trị


Khi đó, các giá trị của x là 6 hoặc 84
Ta lại có 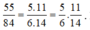
Do đó, ![]() hoặc ngược lại
hoặc ngược lại
Vậy xác suất để lấy được hai viên bi đỏ là
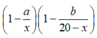
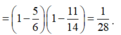
Đúng 0
Bình luận (0)
Từ các chữ số {0, 3, 4, 5, 6, 7} có thể lập được bao nhiêu số tự nhiên chẵn gồm 4 chữ số khác nhau ?
Số cần tìm có dạng \(\overline{abcd}\left(a,b,c,d\in\left\{0;3;4;5;6;7\right\}\right)\)
TH1: \(d=0\)
a có 5 cách chọn
b có 4 cách chọn
c có 3 cách chọn
\(\Rightarrow\) Có \(3.4.5=60\) cách lập.
TH2: \(d\ne0\)
d có 2 cách chọn
a có 4 cách chọn
b có 4 cách chọn
c có 3 cách chọn
\(\Rightarrow\) Có \(2.3.4.4=96\) cách lập.
Vậy có \(96+60=156\) cách lập.
Đúng 1
Bình luận (0)















