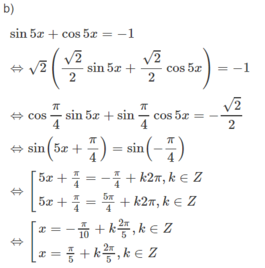Giải phương trình \(\dfrac{Sin5x}{5Sinx}=1\)

Những câu hỏi liên quan
giải các phương trình sau
a) \(sin5x=sinx\)
b) \(cos\left(x+\dfrac{\pi}{3}\right)=-\dfrac{1}{2}\)
a: sin 5x=sin x
=>\(\left[{}\begin{matrix}5x=x+k2\Omega\\5x=\Omega-x+k2\Omega\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}4x=k2\Omega\\6x=\Omega+k2\Omega\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=\dfrac{k\Omega}{2}\\x=\dfrac{\Omega}{6}+\dfrac{k\Omega}{3}\end{matrix}\right.\)
b; \(cos\left(x+\dfrac{\Omega}{3}\right)=-\dfrac{1}{2}\)
=>\(\left[{}\begin{matrix}x+\dfrac{\Omega}{3}=\dfrac{2}{3}\Omega+k2\Omega\\x+\dfrac{\Omega}{3}=-\dfrac{2}{3}\Omega+k2\Omega\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=\dfrac{1}{3}\Omega+k2\Omega\\x=-\Omega+k2\Omega\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Sin5x/5sinx=1
(sin5x)/(5sinx)=1 (dk: sinx khac 0)
<=> sin5x=5sinx
<=> sin5x - sin4x=4sinx
<=> 2sin2x.cos3x= 4sinx
<=> 4sinx.cosx.cos3x= 4sinx
<=> cosx.cos3x = 1
<=> cosx + cos2x = 2
<=> cos2x = cos4x =1
<=> x = k.bi (loai)
=> vo nghiem
theo minh thi nhu vay
<=> sin5x=5sinx
<=> sin5x - sin4x=4sinx
<=> 2sin2x.cos3x= 4sinx
<=> 4sinx.cosx.cos3x= 4sinx
<=> cosx.cos3x = 1
<=> cosx + cos2x = 2
<=> cos2x = cos4x =1
<=> x = k.bi (loai)
=> vo nghiem
theo minh thi nhu vay
Đúng 0
Bình luận (0)
giải phương trình
a) \(sinx=\dfrac{3}{2}\)
b) \(sinx=\dfrac{\sqrt{2}}{2}\)
c) \(sin7x=sin5x\)
d) \(sin5x=sin45\) độ
a: sin x=3/2
mà -1<=sin x<=1
nên \(x\in\varnothing\)
b; \(sinx=\dfrac{\sqrt{2}}{2}\)
=>sinx=sin(pi/4)
=>x=pi/4+k2pi hoặc x=pi-pi/4+k2pi
=>x=pi/4+k2pi hoặc x=3/4pi+k2pi
c: sin7x=sin5x
=>7x=5x+k2pi hoặc 7x=pi-5x+k2pi
=>2x=k2pi hoặc 12x=pi+k2pi
=>x=kpi hoặc x=pi/12+kpi/6
d: =>5x=45 độ+k*360 độ hoặc 5x=180 độ -45 độ+k*360 độ
=>x=9 độ+k*72 độ hoặc 5x=135 độ+k*360 độ
=>x=9 độ+k*72 độ hoặc x=27 độ+k*72 độ
Đúng 0
Bình luận (0)
Giải các phương trình sau sin5x + cos5x = -1
Giải phương trình : 2sin2x.cos3x-sin5x=0
Tìm m để phương trình sau có nghiệm : 2cos3x-3m+1=0
Mn giải chi tiết ghúp mik nha . Thanks
b: =>cos3x=(3m-1)/2
Để phương trình có nghiệm thì -1<=(3m-1)/2<=1
=>-2<=3m-1<=2
=>-1<=3m<=3
=>-1/3<=m<=1
a: 2*sin2x*cos3x-sin5x=0
=>2*1/2*(sin5x+sin(-x))-sin5x=0
=>sin(-x)=0
=>sin x=0
=>x=kpi
Đúng 2
Bình luận (0)
Giải phương trình cos3x.tan4x sin5x A. B. C. D.
Đọc tiếp
Giải phương trình cos3x.tan4x = sin5x
A. 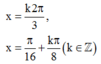
B. 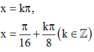
C. 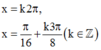
D. 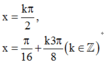
Đáp án B
Phương pháp giải: Quy đồng, đưa về dạng tích và sử dụng công thức tích thành tổng
Lời giải:
Điều kiện: ![]()
Ta có: 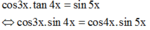
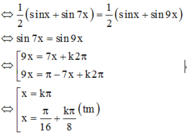
Đúng 0
Bình luận (0)
Giải phương trình cos3x.tan4x sin5x A.
x
k
2
π
3
,
x
π
16
+
k
π
8...
Đọc tiếp
Giải phương trình cos3x.tan4x = sin5x
A. x = k 2 π 3 , x = π 16 + k π 8 ( k ∈ Z )
B. x = k π , x = π 16 + k π 8 ( k ∈ Z )
C. x = k 2 π , x = π 16 + k 3 π 8 ( k ∈ Z )
D. x = k π 2 , x = π 16 + k 3 π 8 ( k ∈ Z )
Đáp án B
Phương pháp giải: Quy đồng, đưa về dạng tích và sử dụng công thức tích thành tổng
Lời giải: Điều kiện: ![]()
Ta có cos3x.tan4x=sin5x ó cos3x.sin4x = cos4x.sin5x
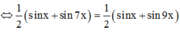
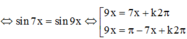
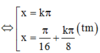
Đúng 0
Bình luận (0)
Giải phương trình cos2x + 5sinx - 4 = 0
![]()
![]()
![]()
![]()
Giải phương trình
cos
2
x
+
5
sin
x
-
4
0
.
A.
x
π
2
+
k
π
B.
x
-
π
2
+
k
π
C.
x
k
2
π
D.
x
π
2...
Đọc tiếp
Giải phương trình cos 2 x + 5 sin x - 4 = 0 .
A. x = π 2 + k π
B. x = - π 2 + k π
C. x = k 2 π
D. x = π 2 + k 2 π
Đáp án D
Phương trình
cos 2 x + 5 sin x - 4 = 0 ⇔ 1 - 2 sin 2 x + 5 sin x - 4 = 0 ⇔ 2 sin 2 x - 5 sin x + 3 = 0 ⇔ 2 sin x - 3 sin x - 1 = 0 ⇔ sin x = 1 ⇔ x = π 2 + k 2 π k ∈ ℤ
Đúng 0
Bình luận (0)