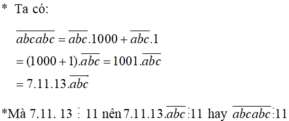abcabc=abc.1001=abc.91.11 chia hết cho 11

tich dung cho minh nha

abcabc = 1001 x abc

            = 11 x 91 x abc

           luôn luôn chia hết cho 11

vì abcabc= abc.1001                                                                                                                                                                    =abc.91.11                                                                                                                                                                                   >abcabc luôn chia hết cho 11

abc abc=abc.1000+abc=abc.(1000+1) 
=abc.1001=abc.91.11 
vì 11 chia hết cho 11=>abc.91.11 chia hết cho 11 
vậy số abcabc lúc nào cũng chia hết cho 11

a ) aaa=a.111=a.(3.37)

          =>aaa bao giờ cũng chia hết cho 37

b) aaaaaa=a.111111=a.(3.37037)

=> aaaaaa bao giờ cũng chia hết cho 3

c) abcabc=abc.1001=abc.(7.13.11)

=> abcabc bao giờ cũng chia hết cho 13;11

d) ab+ba=(10a+b)+(10b+a)=(10a+a)+(10b+b)=11a+11b

=> ab+ba chia hết cho 11

ủng hộ nha

a) aaa = 111a = 37 . 3 . a 

b) aaaaaa = 111111a = 37037 . 3 . a 

c) abcabc = 1001abc = 77.13 . abc 

abcabc = 1001abc = 77.13.abc = 7 .11.13.abc 

d) (ab + ba) = 10a + b + 10b + a =11a + 11b = 11.(a+b) 

a) aaa = a x 100 + a x 10 + a =a x 111 =a x 3 x 37 chia hết cho 37 

b) aaaaaa = a x 111 111 = a x 3037 x 3 cha hết cho 3

c) abc abc = abc   x 1001 = abc x 11 x 13x 7 chia hết cho 11 và 13

d) (ab+ba) = ax10+b + b x10+a=11xa+11xa =11 x(a+b) chia hết cho 11 

abc abc=abc.1000+abc=abc.(1000+1) 
=abc.1001=abc.91.11 
vì 11 chia hết cho 11=>abc.91.11 chia hết cho 11 
vậy số abcabc lúc nào cũng chia hết cho 11

ta co abcabc=1000.abc+abc=abc.1001=91.11.abc

ta co 11 chia hết cho 11 nên abcabc chia hêt cho 11

ta co abcabc = abc . 1001 = 91.11

vì 11 chia hết cho 11 nên abcabc chia hết cho 11

abcabc=abc x 1001=abc x 91 x 11\(⋮\)11

#Châu's ngốc

abcabc

=abc000+abc

=abc.100+abc

=abc.(100+1)

=abc.101

vì 101:101 =>abc.101 chia hết cho 101 =>abcabc luôn chia hết cho 101 với mọi abc

Ta có:abcabc=abc000+abc

=1000abc+abc

=1001.abc

Vì 1001 chia hết cho 11=>1001.abc chai hết cho 11

hay abcabc chia hết cho 11

Vậy abcabc chia hết cho .11

Ta có:

\(\overline{abcabc}=1001\overline{abc}=11.99\overline{abc}\)

Vì \(11.99\overline{abc}\) \(⋮\) 11 nên \(\overline{abcabc}\) \(⋮\) 11

\(\Rightarrow\text{Điều phải chứng minh}\)

Vì x ⋮ 11 <=> (a₀+a₂+a₄+...) - (a₁+a₃+a₅+...) ⋮ 11

=> (c+a+b) - (b+c+a) = 0 ⋮ 11

Vậy dạng abcabc bao giờ cũng chia hết cho 11.

abcabc=a.100000+b.10000+c.1000+a.100+b.10+c.1

=a.100100+b.10010+c.1001

=a00.1001+b0.1001+c.1001

=abc.1001

=(abc.91).11 chia hết cho 11

=> abcabc chia hết cho 11

Theo bài ra ta có :

\(\overline{abcabc}\)

\(=\overline{abc}.1000+\overline{abc}.1\)

\(=\overline{abc}.\left(1000+1\right)\)

\(=\overline{abc}.1001\)

\(=\overline{abc}.11.91\)

\(=\left(\overline{abc}.91\right).11\)

\(\Rightarrow\overline{abcabc}⋮11\left(đpcm\right)\)

Ta có:

\(\overline{abcabc}=1001\overline{abc}=11.91\overline{abc}\)

Vì \(11.91\overline{abc}\) \(⋮\) 11 nên \(\overline{abcabc}\) \(⋮\) 11

\(\Rightarrow\) ĐPCM(điều phải chứng minh)

abcabc \(⋮\) 11 vì:

abcabc = abc . 1000 + abc

abcabc = abc . ( 1000 + 1 )

abcabc = abc . 1001

abcabc = abc . 11 . 91

Mà 11 \(⋮\) 11 \(\Rightarrow\) abc . 11 . 91 \(⋮\) 11

Vậy abcabc \(⋮\) 11 ( đpcm )

Bạn vào câu hỏi tương tự