Cho SABC có SB vuông góc với mặt phẳng ABC, tam giác ABC vuông cân tại A; M là trung điểm của BC; H, K là hình chiếu của B ên SA, SC. Chứng minh rằng:
a, Tam giác SAC vuông
b, AM vuông góc SC
c, BH vuông góc SC
d, SC vuông góc HK
cho hình chóp SABC có đáy tam giác ABC vuông cân tại A, AB=a, SC vuông góc với đáy, SC=a, Mặt phẳng (P) qua C và vuông góc với SB cắt SB tại F và cắt SA tại E. Tính VSCEF
\(BC=AB\sqrt{2}=a\sqrt{2}\)
\(SB=\sqrt{SC^2+BC^2}=a\sqrt{3}\) ; \(SA=\sqrt{SC^2+AC^2}=a\sqrt{2}\)
\(V_{SBAC}=\dfrac{1}{3}SC.\dfrac{1}{2}AB^2=\dfrac{a^3}{6}\)
\(\dfrac{V_{SCEF}}{V_{SABC}}=\dfrac{SF}{SB}.\dfrac{SE}{SA}=\left(\dfrac{SC}{SB}\right)^2\left(\dfrac{SC}{SA}\right)^2=\left(\dfrac{a}{a\sqrt{3}}\right)^2.\left(\dfrac{a}{a\sqrt{2}}\right)^2=\dfrac{1}{6}\)
\(\Rightarrow V_{SCEF}=\dfrac{1}{6}.\dfrac{a^3}{6}=\dfrac{a^3}{36}\)
Cho hình chóp SABC , đáy ABC là tam giác vuông cân AB=AC=a, SC⊥(ABC), SC=a, Mặt phẳng qua C vuông góc với SB cắt SA,SB tại E và F. Tính VSCEF.
a,Tính góc giữa SC và ( ABC)
b, Tính góc giữa ( SBC ) Và ( ABC)
Biết:
1,Hình chóp SABC có đáy ABC là tam giác đều cạnh bằng a, tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với đáy, SB hợp với đáy một góc 30 độ
2, Hình chóp SABC có đáy ABC là tam giác đều , mặt bên SAB nằm trong mặt phẳng vuông góc với mặt phẳng đáy và tam giác SAB vuông tại S. SA= \(a\sqrt{3}\), SB= a
Cho tứ diện SABC có SA vuông góc với mặt phẳng (ABC) và tam giác ABC vuông tại B. Trong mp(SAB), kẻ AM vuông góc với SB tại M. Trên cạnh SC lấy điểm N sao cho SM/SB = SN/SC .
Chứng minh rằng:
a) BC ⊥ (SAB), AM ⊥ (SBC)
b) SB ⊥ AN
cho hinh chóp SABC có đáy ABC đều cạnh a,tam giác SAC cân tại S ,mp(SAC) vuông góc với đáy,góc giữa SB và mặt phẳng (ABC) bằng 60,M là trung điểm BC tính d(SM,AC)
cho hình chóp sabcd có đáy là tam giác vuông cân tại a,ab=a√2,sa=sb=sc,góc giữa sa và mặt phẳng(abc )=60 độ.tính thể tích sabc và khoảng cách từ a đến mặt phẳng (sbc)
Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân tại B, AB = a, tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ABC biết góc giữa SB và mặt phẳng (ABC) bằng 450.
A. a 3 3 4
B. a 3 3 12
C. a 3 2 12
D. a 3 2 4
Đáp án C
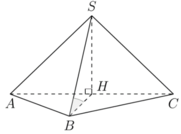
Gọi H là trung điểm AC. Ta có tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với (ABC)
suy ra S H ⊥ A B C
Ta có
S B , A B C = S B H ^ = 45 o ⇒ S H = B H = 1 2 A C = a 2 2 V S . A B C = 1 3 . a 2 2 . 1 2 a 2 = a 3 2 12