Câu 20.

\(C_n^2+C_n^3=4n\)

Đk: \(n\ge3\)

Pt\(\Rightarrow\dfrac{n!}{2!\left(n-2\right)!}+\dfrac{n!}{3!\left(n-3\right)!}=4n\)

   \(\Rightarrow\dfrac{n\left(n-1\right)\left(n-2\right)!}{2\left(n-2\right)!}+\dfrac{n\left(n-1\right)\left(n-2\right)\left(n-3\right)!}{6\left(n-3\right)!}=4n\)

  \(\Rightarrow\dfrac{n\left(n-1\right)}{2}+\dfrac{n\left(n-1\right)\left(n-2\right)}{6}=4n\)

  Chia cả hai vế cho \(n\) ta được:

  \(\Rightarrow\dfrac{n-1}{2}+\dfrac{\left(n-1\right)\left(n-2\right)}{6}=4\)

  Bạn tự quy đồng giải pt bậc hai tìm n nhé.

Câu 21:
\(\frac{1}{2}A^2_{2x}-A^2_x\leq \frac{6}{x}C^3_x+10\)

\(\Leftrightarrow \frac{1}{2}.\frac{(2x)!}{(2x-2)!}-\frac{x!}{(x-2)!}\leq \frac{6}{x}.\frac{x!}{3!(x-3)!}+10\)

\(\Leftrightarrow \frac{1}{2}.2x(2x-1)-(x-1)x\leq (x-1)(x-2)+10\)

\(\Leftrightarrow 12-3x\geq 0\Leftrightarrow x\leq 4\)

Mà $x$ tự nhiên, $x\geq 3$ nên $x=3, x=4$

Đáp án C. 

Câu 20:

\(C^2_n+C^3_n=4n\)

\(\Leftrightarrow\dfrac{n.\left(n-1\right)}{2!}+\dfrac{4.\left(n-1\right).\left(n-2\right)}{3!}=4n\)

\(\Leftrightarrow\dfrac{n.\left(n-1\right)}{2}+\dfrac{n.\left(n-1\right).\left(n-2\right)}{6}=4n\)

\(\Leftrightarrow3n.\left(n-1\right)+n.\left(n-1\right).\left(n-2\right)=24n\)

\(\Leftrightarrow3n^2-3n+n.\left(n^2-3n+2\right)-24n=0\)

\(\Leftrightarrow n^3-25n=0\)

\(\Leftrightarrow n.\left(n^2-25\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}n=0\\n^2=25\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}n=0\\\left[{}\begin{matrix}n=5\\n=-5\end{matrix}\right.\end{matrix}\right.\)

14. B

19. C

20. A

21. A

22. D

23. B

CÂU :14. B

CÂU:19. C

CÂU:20. A

CÂU:21. A

22. D

23. B

12.

\(y=\sqrt{2}sin\left(2x+\dfrac{\pi}{4}\right)\le\sqrt[]{2}\)

\(\Rightarrow M=\sqrt{2}\)

13.

Pt có nghiệm khi:

\(5^2+m^2\ge\left(m+1\right)^2\)

\(\Leftrightarrow2m\le24\)

\(\Rightarrow m\le12\)

14.

\(\Leftrightarrow\left[{}\begin{matrix}cosx=1\\cosx=-\dfrac{5}{3}\left(loại\right)\end{matrix}\right.\)

\(\Leftrightarrow x=k2\pi\)

15.

\(\Leftrightarrow\left[{}\begin{matrix}tanx=-1\\tanx=3\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{4}+k\pi\\x=arctan\left(3\right)+k\pi\end{matrix}\right.\)

Đáp án A

16.

\(\dfrac{\sqrt{3}}{2}sinx-\dfrac{1}{2}cosx=\dfrac{1}{2}\)

\(\Leftrightarrow sin\left(x-\dfrac{\pi}{6}\right)=\dfrac{1}{2}\)

\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{6}=\dfrac{\pi}{6}+k2\pi\\x-\dfrac{\pi}{6}=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k2\pi\\x=\pi+k2\pi\end{matrix}\right.\)

\(\left[{}\begin{matrix}2\pi\le\dfrac{\pi}{3}+k2\pi\le2018\pi\\2\pi\le\pi+k2\pi\le2018\pi\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}1\le k\le1008\\1\le k\le1008\end{matrix}\right.\)

Có \(1008+1008=2016\) nghiệm

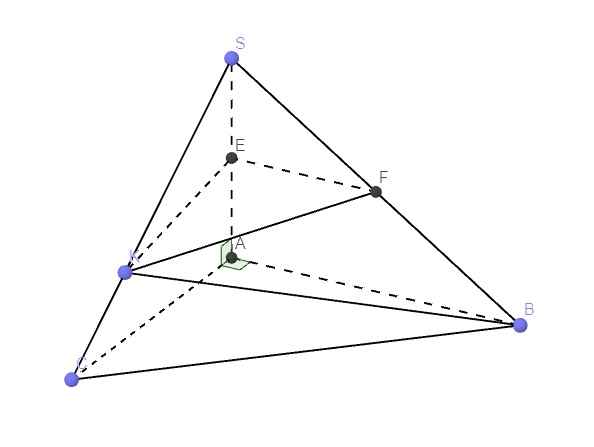
21.

\(\left\{{}\begin{matrix}SA\perp AB\\AC\perp AB\end{matrix}\right.\) \(\Rightarrow AB\perp\left(SAC\right)\)

E là trung điểm SA, F là trung điểm SB \(\Rightarrow\) EF là đường trung bình tam giác SAB

\(\Rightarrow EF||AB\Rightarrow EF\perp\left(SAC\right)\)

\(\Rightarrow EF=d\left(F;\left(SEK\right)\right)\)

\(SE=\dfrac{1}{2}SA=\dfrac{3a}{2}\) ; \(EF=\dfrac{1}{2}AB=a\)

 \(SC=\sqrt{SA^2+AC^2}=a\sqrt{13}\Rightarrow SK=\dfrac{2}{3}SC=\dfrac{2a\sqrt{13}}{3}\)

\(\Rightarrow S_{SEK}=\dfrac{1}{2}SE.SK.sin\widehat{ASC}=\dfrac{1}{2}.\dfrac{3a}{2}.\dfrac{2a\sqrt{13}}{3}.\dfrac{2a}{a\sqrt{13}}=a^2\)

\(\Rightarrow V_{S.EFK}=\dfrac{1}{3}EF.S_{SEK}=\dfrac{1}{3}.a.a^2=\dfrac{a^3}{3}\)

\(AB\perp\left(SAC\right)\Rightarrow AB\perp\left(SEK\right)\Rightarrow AB=d\left(B;\left(SEK\right)\right)\)

\(\Rightarrow V_{S.EBK}=\dfrac{1}{3}AB.S_{SEK}=\dfrac{1}{3}.2a.a^2=\dfrac{2a^3}{3}\)

22.

Gọi D là trung điểm AB

Do tam giác ABC đều \(\Rightarrow CD\perp AB\Rightarrow CD\perp\left(SAB\right)\)

\(\Rightarrow CD=d\left(C;\left(SAB\right)\right)\)

\(CD=\dfrac{AB\sqrt{3}}{2}=a\sqrt{3}\) (trung tuyến tam giác đều)

N là trung điểm SC \(\Rightarrow d\left(N;\left(SAB\right)\right)=\dfrac{1}{2}d\left(C;\left(SAB\right)\right)=\dfrac{a\sqrt{3}}{2}\)

\(S_{SAB}=\dfrac{1}{2}SA.AB=a^2\sqrt{3}\) \(\Rightarrow S_{SAM}=\dfrac{1}{2}S_{SAB}=\dfrac{a^2\sqrt{3}}{2}\)

\(\Rightarrow V_{SAMN}=\dfrac{1}{3}.\dfrac{a\sqrt{3}}{2}.\dfrac{a^2\sqrt{3}}{2}=\dfrac{a^3}{4}\)

Lại có:

\(V_{SABC}=\dfrac{1}{3}SA.S_{ABC}=\dfrac{1}{3}.a\sqrt{3}.\dfrac{\left(2a\right)^2\sqrt{3}}{4}=a^3\)

\(\Rightarrow V_{A.BCMN}=V_{SABC}-V_{SANM}=\dfrac{3a^3}{4}\)

Hình vẽ câu 21:

 
 a.chia cho 15 dư 1
 
b. chia cho 15 dư 14
 
 c.chia hết cho 81

k mình nha

chia 15 dư 1

chia cho 15 dư 14

chia hết cho 81 

tích mk đi dù chỉ 1 cái

a) Chia hết cho 15 dư 1

b) chia 15 dư 14

c) chia hết 81

Câu nào bạn, nếu mà cả thì đăng tách ra đi :)