Chứng minh rằng =
khi và chỉ khi trung điểm của hai đoạn thẳng AD và BC trùng nhau.

Những câu hỏi liên quan
Chứng minh rằng 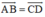 khi và chỉ khi trung điểm của hai đoạn thẳng AD và BC trùng nhau.
khi và chỉ khi trung điểm của hai đoạn thẳng AD và BC trùng nhau.
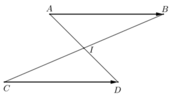
Gọi trung điểm của AD là I, trung điểm BC là J.
Khi đó ta có: 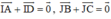
Mà theo quy tắc ba điểm ta có:
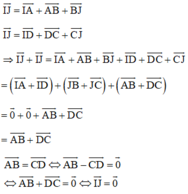
⇔ I ≡ J hay trung điểm AD và BC trùng nhau (đpcm)
Đúng 0
Bình luận (0)
Cho bốn điểm A, B, C, D. Chứng minh rằng \(\overrightarrow {AB} = \overrightarrow {CD} \) khi và chỉ khi trung điểm của hai đoạn thẳng AD và BC trùng nhau.
Với 4 điểm A, B, C, D ta có: \(\overrightarrow {AB} = \overrightarrow {CD} \) khi và chỉ khi tứ giác ABDC là hình bình hành
Theo tính chất của hình bình hành thì giao điểm của hai đường chéo là trung điểm của mỗi đường và ngược lại.
Nói cách khác: trung điểm của hai đoạn thẳng AD và BC trùng nhau.
Vậy ta có điều phải chứng minh.
Đúng 0
Bình luận (0)
Với 4 điểm A, B, C, D ta có: \(\overrightarrow {AB} = \overrightarrow {CD} \) khi và chỉ khi tứ giác ABDC là hình bình hành
Theo tính chất của hình bình hành thì giao điểm của hai đường chéo là trung điểm của mỗi đường và ngược lại.
Nói cách khác: trung điểm của hai đoạn thẳng AD và BC trùng nhau.
Vậy ta có điều phải chứng minh.
Đúng 0
Bình luận (0)
Chứng minh rằng \(\overrightarrow{AB}=\overrightarrow{CD}\) khi và chỉ khi trung điểm của hai đoạn thẳng AD và BC trùng nhau ?
Nếu \(\overrightarrow{AB}=\overrightarrow{CD}\) thì AD và BC có trung điểm trùng nhau. Gọi I là trung điểm của AD ta chứng minh I cũng là trung điểm của BC.
Theo quy tắc của ba điểm của tổng, ta có
\(\overrightarrow{AB}=\overrightarrow{AI}+\overrightarrow{IB};\overrightarrow{CD}=\overrightarrow{CI}+\overrightarrow{ID}\)
Vì \(\overrightarrow{AB}=\overrightarrow{CD}\) nên \(\overrightarrow{AI}+\overrightarrow{IB}=\overrightarrow{CI}+\overrightarrow{ID}\)
\(\Rightarrow\overrightarrow{AI}-\overrightarrow{ID}=\overrightarrow{CI}-\overrightarrow{IB}\)
\(\Rightarrow\overrightarrow{AI}+\overrightarrow{DI}=\overrightarrow{CI}+\overrightarrow{BI}\left(1\right)\)
Vì I là trung điểm của AD nên \(\overrightarrow{AI}+\overrightarrow{DI}=\overrightarrow{0}\left(2\right)\)
Từ (1) và (2) suy ra \(\overrightarrow{CI}+\overrightarrow{BI}=\overrightarrow{0}\left(3\right)\)
Từ (3) ta có chung điểm I, ta chứng minh \(\overrightarrow{AB}=\overrightarrow{CD}\)
I là trung điểm AD \(\Rightarrow\overrightarrow{AI}+\overrightarrow{DI}=\overrightarrow{0}\Rightarrow\overrightarrow{AI}-\overrightarrow{ID}=\overrightarrow{0}\)
I là trung điểm BC \(\Rightarrow\overrightarrow{CI}+\overrightarrow{BI}=0\Rightarrow\overrightarrow{CI}-\overrightarrow{IB}=\overrightarrow{0}\)
Suy ra \(\overrightarrow{AI}-\overrightarrow{ID}=\overrightarrow{CI}-\overrightarrow{IB}\)
\(\Rightarrow\overrightarrow{AI}+\overrightarrow{IB}=\overrightarrow{CI}+\overrightarrow{ID}\Rightarrow\overrightarrow{AB}=\overrightarrow{CD}\)
Đúng 0
Bình luận (0)
Bài 1:Chứng minh rằng :M là trung điểm của đoạn thẳng AB khi và chỉ khi \(MA=MB=\frac{1}{2}AB\)
Bài 2 Bốn điểm A,B ,C,D cùng nằm trên một đường thẳng và AB, CD có cùng trung điểm
Chứng tỏ rằng : AC=BD và AD=BC
Bài 1 :
a) M là trung điểm của đoạn thẳng AB
\(\Rightarrow MA=MB=\frac{1}{2}AB\). Thật vậy : Do M là trung điểm của AB nên theo đĩnh nghĩa ta có
:\(MA+MB=AB\)VÀ \(MA=MB\)
\(\Rightarrow2MA=2MB=AB\)
\(\Rightarrow MA=MB\frac{1}{2}AB\)
b) Nếu \(MA=MB=\frac{1}{2}AB\Rightarrow\)M là trung điểm của đoạn thằng AB
Từ \(MA=MB=\frac{1}{2}AB\Rightarrow MA+MB=\frac{1}{2}AB+\frac{1}{2}AB=AB\)
Vậy \(MA+MB=AB\)VÀ \(MA=MB\)
Chứng tỏ M là trung điểm đoạn thẳng AB
Bài 2 :
Gọi O là trung điểm chung của AB VÀ CD. Ta có:
Gỉa sử :A và C cùng phía đối với O
Ta thấy rằng
\(\hept{\begin{cases}AC=OC-OA\\BD=OD-OB\end{cases}}\)
\(\Leftrightarrow\)\(AC=BD\)
\(\hept{\begin{cases}AD=OA+OD\\BC=OB+OC\end{cases}}\)
\(\Leftrightarrow AD=BC\)
Trường hợp A,C khác phía đối với O chứng minh tương tự
Mk k vẽ được hình xin lỗi bạn nhiều nha!
Chúc bạn học tốt ( -_- )
Đúng 1
Bình luận (0)
cho 4 điểm A,B,C,D theo thứ tự đó và nằm trên 1 đường thẳng.Biết AB=12cm,BC=20cm,CD=12cm
1)chứng minh rằng AC=BD
2)chứng minh rằng trung điểm của đoạn thẳng AD trùng với trung điểm của đoạn thẳng BC
Hai đoạn thẳng AB và CD cắt nhau tại trung điểm O của mỗi đoạn thẳng . Chứng minh rằng AD // BC
Xét tam giác ADO và tam giác CBO có :
O1 = O2 ( đối đỉnh )
CO = OD ( gt )
AO = OB ( gt )
Suy ra tam giác ADO = tam giác CBO
=> \(\widehat{ADO}=\widehat{OCB}\)( 2 góc tương ứng ) mà 2 góc này ở vị trí so le trong
=> AD // BC
Đúng 0
Bình luận (0)
Cho AC và BD cắt nhau tại trugn điểm O của mỗi đoạn. M và N là trung điểm của BC và AD. Chứng minh rằng : O là trung điểm của MN. ( Chỉ cần giúp mình đến bước chứng minh 3 điểm O, M, N thẳng hàng thôi nhé)
Xét \(\Delta\)AOD & \(\Delta\)COB có:
OA=OC(vì O là trung điểm AC)
góc AOD= góc COB(2 góc đối đỉnh)
OD=OB(vì O là trung điểm BD)
=>\(\Delta\)AOD=\(\Delta\)COB(c.g.c)
=>AD=CB(2 cạnh tương ứng)(1)
Vì N là trung điểm của AD
=>AN=ND=AD/2(2)
Vì M là trung điểm BC
=>MB=MC=BC/2(3)
Từ (1);(2);(3)=>AN=MC
Xét \(\Delta\)NOA & \(\Delta\)MOC có:
AN=MC(theo c/m trên)
ON=OM(vì O là trung điểm MN)
OA=ỌC(vì O là trung điểm AC)
=>\(\Delta\)NOA=\(\Delta\)MOC(c.c.c)
=>góc NOA= góc MOV(2 góc tương ứng)
Ta có: góc =180 độ
=>góc NOA+ góc NOC= 180 độ(2 góc kề bù)
=>góc MOC+góc NỚC=180 độ
=>góc NOM=180 độ
=>N,O,M thẳng hàng
Đúng 0
Bình luận (0)
Chứng minh AC→ = BD→ khi và chỉ khi trung điểm của 2 đoạn thẳng AD và BC trùng nhau
Xét tứ giác ABDC có
AD cắt BC tại trung điểm của mỗi đường
nên ABDC là hình bình hành
Suy ra: vecto AC=vecto BD
Đúng 0
Bình luận (0)
Cho hai đoạn thẳng AB và CD cắt nhau tại trung điểm O của mỗi đoạn thẳng . Lấy các điểm E trên đoạn thẳng AD ; F trên đoạn thẳng bc sao cho AE=BF . chứng minh rằng ÈO thẳng hàng
Bài 12. Cho hai đoạn thẳng AB và CD cắt nhau tại trung điểm O của mỗi đoạn thẳng. Lấy các điểm E trên đoạn AD, F trên đoạn BC sao cho AE = BF. Chứng minh rằng E,O,F thẳng hàng.



















