Chứng minh rằng hàm số y đồng biến trên khoảng (0 ; 1) và nghịch biến trên các khoảng (1 ; 2).
Đọc tiếp
Chứng minh rằng hàm số y = đồng biến trên khoảng (0 ; 1) và nghịch biến trên các khoảng (1 ; 2).
Những câu hỏi liên quan
Chứng minh rằng hàm số y = 2 x - x 2 đồng biến trên khoảng (0; 1), nghịch biến trên khoảng (1; 2).
TXĐ: D = [0; 2]
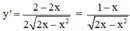
+ Hàm số đồng biến
⇔ y’ > 0
⇔ 0 < x < 1.
+ Hàm số nghịch biến
⇔ y’ < 0
⇔ 1 < x < 2.
Vậy hàm số đồng biến trên khoảng (0; 1), nghịch biến trên khoảng (1; 2).
Đúng 0
Bình luận (0)
Chứng minh rằng hàm số \(y=\sqrt{2x-x^2}\) đồng biến trên khoảng (0 ; 1) và nghịch biến trên các khoảng (1 ; 2).
Tập xác định : D = [0 ; 2]; y' = , ∀x ∈ (0 ; 2); y' = 0 ⇔ x = 1.
Bảng biến thiên :
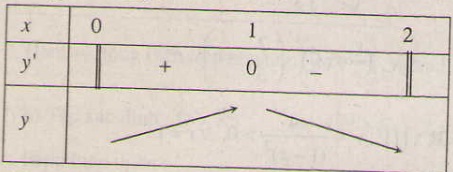
Vậy hàm số đồng biến trên khoảng (0 ; 1) và nghịch biến trên khoảng (1 ; 2).
Đúng 0
Bình luận (0)
Chứng minh rằng hàm số y = x x 2 + 1 đồng biến trên khoảng (-1; 1), nghịch biến trên khoảng (-∞; -1) và (1; +∞).
TXĐ: D = R
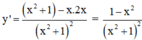
+ Hàm số nghịch biến
⇔ y’ < 0
⇔ 1 – x2 < 0
⇔ x2 > 1
⇔ x ∈ (-∞ ; -1) ∪ (1; +∞).
+ Hàm số đồng biến
⇔ y’ > 0
⇔ 1 – x2 > 0
⇔ x2 < 1
⇔ x ∈ (-1; 1).
Vậy hàm số đồng biến trên khoảng (-1; 1) và nghịch biến trên các khoảng (-∞; -1) và (1; +∞).
Đúng 0
Bình luận (0)
Chứng minh rằng hàm số đồng biến trên khoảng (-1; 1), nghịch biến trên khoảng (-∞; -1) và (1; +∞).
Đọc tiếp
Chứng minh rằng hàm số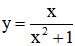 
đồng biến trên khoảng (-1; 1), nghịch biến trên khoảng (-∞; -1) và (1; +∞).
Cho hàm số y = m x - 1 2 x + m
Chứng minh rằng với mọi giá trị của tham số m, hàm số luôn đồng biến trên khoảng xác định của nó.
Với mọi tham số m ta có :
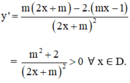
Vậy hàm số luôn đồng biến trên mỗi khoảng xác định của nó.
Đúng 0
Bình luận (0)
Chứng minh tính đơn điệu của hàm số y=cos x đồng biến trên khoảng \(\left(-\pi+k2\pi;0+k2\pi\right)\)
Chứng minh rằng hàm số \(y=\dfrac{x^2}{x^2+1}\) đồng biến trên khoảng (-1 ; 1) và nghịch biến trên các khoảng (-∞ ; -1) và (1 ; +∞).
Tập xác định : D = R. y' =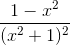 
=> y' = 0 ⇔ x=-1 hoặc x=1.
Bảng biến thiên :
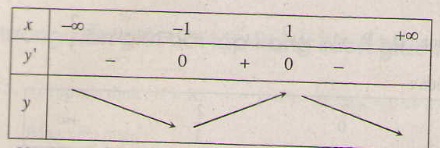
Vậy hàm số đồng biến trên khoảng (-1 ; 1); nghịch biến trên các khoảng (-∞ ; -1), (1 ; +∞).
Đúng 0
Bình luận (0)
Cho hàm số y = ( a 2 - 2a + 4)x - 9
Chứng minh rằng hàm số trên đồng biến trên R
y = ( a 2 - 2a + 4)x - 9
Ta có: a 2 - 2a + 4 = a 2 - 2a + 1 + 3 = a - 1 2 + 3 > 0 ∀a
Vậy hàm số luôn đồng biến trên R
Đúng 0
Bình luận (0)
cho hàm số y=f(x)=-x^2-2x+1. Mệnh đề nào sau đây là đúng? A. Hàm số nghịch biến trên khoảng (-1;+vô cực) B. Hàm số nghịch biến trên khoảng (-vô cực;-1) C. Hàm số đồng biến trên khoảng (-1;+vô cực) D. Hàm số đồng biến trên khoảng (-vô cực;0)
B. Hàm số nghịch biến trên khoảng \(\left(-\infty;-1\right)\)
Đúng 3
Bình luận (0)
Cho hàm số
y
f
(
x
)
có đạo hàm trên khoảng
a
;
b
. Xét các mệnh đề sau: I. Nếu hàm số
y
f
(
x
)
đồng biến trên khoảng
a
;
b
thì
f...
Đọc tiếp
Cho hàm số y = f ( x ) có đạo hàm trên khoảng a ; b . Xét các mệnh đề sau:
I. Nếu hàm số y = f ( x ) đồng biến trên khoảng a ; b thì f ' x > 0 , ∀ x ∈ a ; b .
II. Nếu f ' x < 0 , ∀ x ∈ a ; b thì hàm số y = f ( x ) nghịch biến trên khoảng a ; b .
III. Nếu hàm số y = f ( x ) liên tục trên a ; b và f ' x > 0 , ∀ x ∈ a ; b thì hàm số y = f ( x ) đồng biến trên đoạn a ; b .
Số mệnh đề đúng là:
A. 3
B. 0
C. 2
D. 1
Đáp án là C
I.Sai ví dụ hàm số y = x 3 đồng biến trên
(−¥; +¥) nhưng y' ³ 0, "x Î (−¥; +¥)
II.Đúng
III.Đúng
Đúng 0
Bình luận (0)