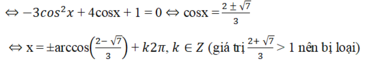Giải phương trình 4cos^3 x - 4cosx -sinx.cosx+1=0
Những câu hỏi liên quan
Số vị trí biểu diễn các nghiệm của phương trình : \(4cos^2x-4cosx-3=0\) trên đường tròn lượng giác là ?
A . 2
B . 0
C . 1
D . 4
Xem thêm câu trả lời
Giải phương trình sau: 2sin2 x + sinx.cosx – 3cos2 x = 0
2sin2x + sinx.cosx – 3cos2x = 0 (1)
+ Xét cos x = 0 ⇒ sin2x = 1 – cos2x = 1
Phương trình (1) trở thành: 2 = 0 (loại)
+ Xét cos x ≠ 0, chia cả hai vế của (1) cho cos2x ta được:
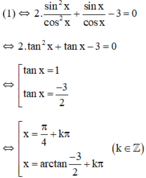
Vậy phương trình có tập nghiệm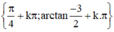 
(k ∈ Z)
Đúng 0
Bình luận (0)
Giải các phương trình sau:
\(a,cos2x+4cosx+1=0\)
\(b,cos^22x=\dfrac{1}{4}\)
a, \(cos2x+4cosx+1=0\)
\(\Leftrightarrow2cos^2x+4cosx=0\)
\(\Leftrightarrow2cosx\left(cosx+2\right)=0\)
\(\Leftrightarrow cosx=0\)
\(\Leftrightarrow x=\dfrac{\pi}{2}+k\pi\)
Đúng 2
Bình luận (0)
b, \(cos^22x=\dfrac{1}{4}\)
\(\Leftrightarrow4cos^22x-1=0\)
\(\Leftrightarrow\left(2cosx-1\right)\left(2cosx+1\right)=0\)
\(\Leftrightarrow cosx=\pm\dfrac{1}{2}\)
\(\Leftrightarrow x=\pm\dfrac{\pi}{3}+k\pi\)
Đúng 1
Bình luận (0)
Giải phương trình sau: 3 sin 2 x + 4 cos x - 2 = 0
Giải các phương trình lượng giác sau:
1) \(2cos^2\left(x+\dfrac{2\pi}{3}\right)-1=0\)
2) \(4cos^2\left(x+\dfrac{\pi}{6}\right)-3=0\)
3) \(8cos^3\left(2x-\dfrac{\pi}{6}\right)-3\sqrt{3}=0\)
1.
\(\Leftrightarrow cos\left(2x+\dfrac{4\pi}{3}\right)=0\)
\(\Leftrightarrow2x+\dfrac{4\pi}{3}=\dfrac{\pi}{2}+k\pi\)
\(\Leftrightarrow2x=-\dfrac{5\pi}{6}+k\pi\)
\(\Leftrightarrow x=-\dfrac{5\pi}{12}+\dfrac{k\pi}{2}\)
b.
\(\Leftrightarrow2+2cos\left(2x+\dfrac{\pi}{3}\right)-3=0\)
\(\Leftrightarrow cos\left(2x+\dfrac{\pi}{3}\right)=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+\dfrac{\pi}{3}=\dfrac{\pi}{3}+k2\pi\\2x+\dfrac{\pi}{3}=-\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k\pi\\x=-\dfrac{\pi}{3}+k\pi\end{matrix}\right.\)
c.
\(\Leftrightarrow cos\left(2x-\dfrac{\pi}{6}\right)=\dfrac{\sqrt{3}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-\dfrac{\pi}{6}=\dfrac{\pi}{6}+k2\pi\\2x-\dfrac{\pi}{6}=-\dfrac{\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k\pi\\x=k\pi\end{matrix}\right.\)
Đúng 2
Bình luận (1)
Với giá trị nào của m để phương trình
m
.
sin
2
x
-
3
.
sin
x
.
cos
x
-
m
-
1
có đúng 3 nghiệm
x
∈
0
,
...
Đọc tiếp
Với giá trị nào của m để phương trình m . sin 2 x - 3 . sin x . cos x - m - 1 có đúng 3 nghiệm x ∈ 0 , 3 π 2 ?
Phương trình :
sin
2
x
-
(
3
+
1
)
sin
x
.
cos
x
+
3
cos
2
x
0
có họ nghiệm là
Đọc tiếp
Phương trình : sin 2 x - ( 3 + 1 ) sin x . cos x + 3 cos 2 x = 0 có họ nghiệm là
Hướng dẫn giải:
Chọn D.
không là nghiệm của phương trình
Chia 2 vế phương trình cho cos2x ta được
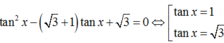
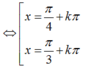
Đúng 0
Bình luận (0)
Giải phương trình sau: 3sin2 x – 4 sinx.cosx + 5 cos2 x =2
3sin2x – 4sinx.cosx + 5cos2x = 2
⇔ 3sin2x – 4sinx.cosx + 5cos2x = 2(sin2x + cos2x)
⇔ sin2x – 4sinx.cosx + 3 cos2x = 0 (1)
+ Xét cosx = 0 ⇒ sin2x = 1.
Phương trình (1) trở thành 1 = 0 (Vô lý).
+ Xét cos x ≠ 0. Chia hai vế phương trình cho cos2x ta được
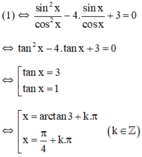
Vậy phương trình có tập nghiệm
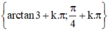(k ∈ Z)
Đúng 0
Bình luận (0)
Giải phương trình: 3sinx - 4cosx = 1
3sinx – 4cosx = 1 ⇔ 3/5sinx - 4/5cosx = 1/5.
⇔ sin(x – α) = 1/5 (với cosα = 3/5 , sinα = 4/5)
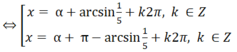
Đúng 0
Bình luận (0)