Giải giùm em với ạ

Những câu hỏi liên quan
Mọi người giải giúp em bài này với ạ sẵn giải thích giùm em luôn ạ . Giải nhanh giúp em. Em cảm ơn. 
III.
A.
1. B
2. C
3. B
4. A
5. D
B.
1. C
2. B
3. B
4. A
5. C
Đúng 2
Bình luận (0)
1 b c b a d
2 c b b a c nha
Mọi người giải giúp em đề này với ạ sẵn giải thích giùm em luôn ạ. Giải nhanh giúp em. Em cảm ơn. 
Đề dài thế này sao giải thích nhanh cho e đc
Part 1
1 C
2 B
3 D
4 C
5 B
6 A
Part 2
1 T
2 F
3 F
4 F
V
1 That old house has just been bought
2 If he doesn't take these pills, he won't be better
3 I suggest taking a train
4 Spending the weekend in the countryside is very wonderful
Đúng 2
Bình luận (0)
giải giùm em với ạ

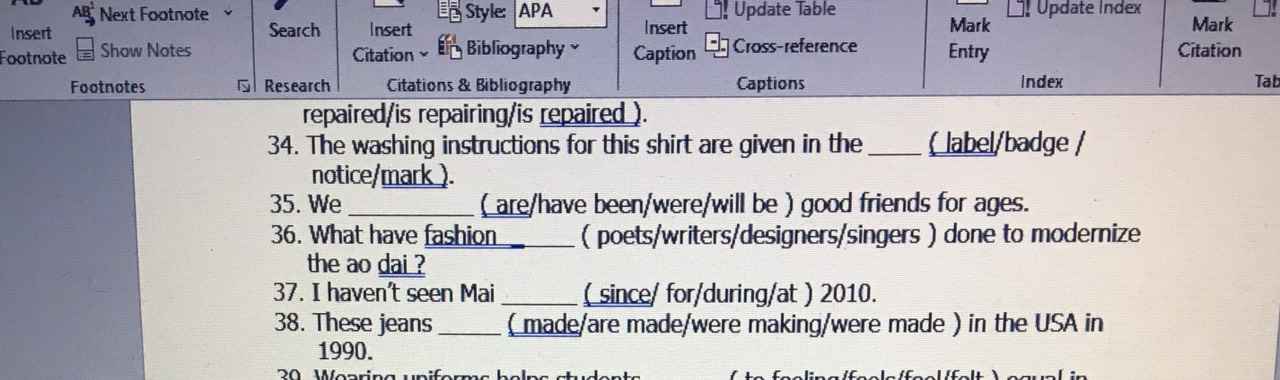
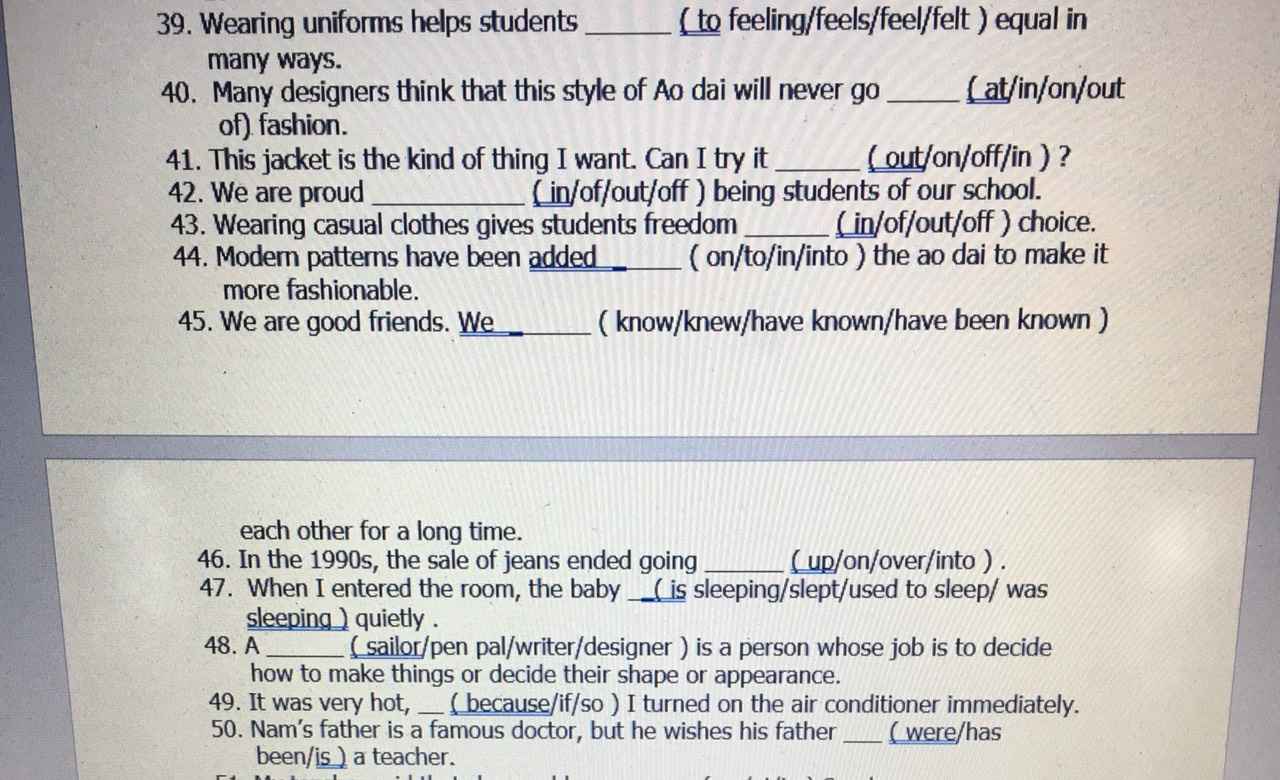
giải giùm em gấp câu 2 với ạ em cần rất gấp em cảm ơn ạ
Đọc tiếp
giải giùm em gấp câu 2 với ạ em cần rất gấp em cảm ơn ạ
Giải giùm em với ạ , em đang cần gấp
VI
1 scientist
2 scientism
3 interesting
4 to take
5 would be
6 don't
7 flying
8 had
9 unidentified
10 imagination
11 interested
12 electricity
13 evidence
14 at - on
15 entertainment
16 were
17 would write
18 appearance
Đúng 2
Bình luận (0)
Giải nhanh giùm em với ạ
Giải ra giùm em với ạ
Mn giúp em giải giùm em với ạ. Em cảm ơn
a,
Xét Δ ABH và Δ CBA, có :
\(\widehat{ABH}=\widehat{CAB}\) (góc chung)
\(\widehat{AHB}=\widehat{CAB}=90^o\)
=> Δ ABH ~ Δ CBA (g.g)
=> \(\dfrac{AB}{CB}=\dfrac{BH}{BA}\)
=> \(AB^2=BH.BC\)
Xét Δ ABC vuông tại A, có :
\(BC^2=AB^2+AC^2\) (Py - ta - go)
=> \(BC^2=15^2+20^2\)
=> BC = 25 (cm)
Ta có : \(AB^2=BH.BC\) (cmt)
=> \(15^2=BH.25\)
=> BH = 9 (cm)
Ta có : BC = BH + CH
=> 25 = 9 + CH
=> CH = 16 (cm)
Đúng 2
Bình luận (0)
b,
Xét Δ AMN và Δ ACB, có :
\(\widehat{MAN}=\widehat{CAB}=90^o\)
\(\widehat{MAN}=\widehat{CAB}\) (góc chung)
=> Δ AMN ~ Δ ACB (g.g)
=> \(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
=> AM.AB = AN.AC
Ta có : \(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
=> \(\dfrac{AB}{AC}=\dfrac{AN}{AM}\)
=> \(\dfrac{AN}{AM}=\dfrac{15}{20}=\dfrac{3}{4}\)
Vậy : ta có kết luận : Δ AMN = \(\dfrac{3}{4}\) Δ ACB
Đúng 1
Bình luận (0)
Xem thêm câu trả lời

Mọi người giải giúp em với ạ, mai em thi rồi, mấy anh/chị giải thích rõ ràng giùm em nhé, em cảm ơn ạ.
Bài `13`
\(a,\sqrt{27}+\sqrt{48}-\sqrt{108}-\sqrt{12}\\ =\sqrt{9\cdot3}+\sqrt{16\cdot3}-\sqrt{36\cdot3}-\sqrt{4\cdot3}\\ =3\sqrt{3}+4\sqrt{3}-6\sqrt{3}-2\sqrt{3}\\ =\left(3+4-6-2\right)\sqrt{3}\\ =-\sqrt{3}\\ b,\left(\sqrt{28}+\sqrt{12}-\sqrt{7}\right)\cdot\sqrt{7}+\sqrt{84}\\ =\left(\sqrt{4\cdot7}+\sqrt{4\cdot3}-\sqrt{7}\right)\cdot\sqrt{7}+\sqrt{4\cdot21}\\ =\left(2\sqrt{7}+2\sqrt{3}-\sqrt{7}\right)\cdot\sqrt{7}+2\sqrt{21}\\ =2\cdot7+2\sqrt{21}-7+2\sqrt{21}\\ =14+2\sqrt{21}-7+2\sqrt{21}\\ =7+4\sqrt{21}\)
Đúng 0
Bình luận (1)
17:
ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x< >4\end{matrix}\right.\)
Để A là số nguyên thì \(\sqrt{x}-1⋮\sqrt{x}-2\)
=>\(\sqrt{x}-2+1⋮\sqrt{x}-2\)
=>\(\sqrt{x}-2\in\left\{1;-1\right\}\)
=>\(\sqrt{x}\in\left\{3;1\right\}\)
=>\(x\in\left\{9;1\right\}\)
16:
a: BC=BH+CH
=9+16
=25(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\)
=>\(AH=\sqrt{9\cdot16}=12\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=\sqrt{9\cdot25}=15\left(cm\right)\\AC=\sqrt{16\cdot25}=20\left(cm\right)\end{matrix}\right.\)
b: M là trung điểm của AC
=>AM=AC/2=10(cm)
Xét ΔAMB vuông tại A có
\(tanAMB=\dfrac{AB}{AM}=\dfrac{15}{10}=\dfrac{3}{2}\)
nên \(\widehat{AMB}\simeq56^0\)
Đúng 0
Bình luận (0)






















