giải bất phương trình sau : \(\frac{-3x+1}{2x+1}\le-2\)
giải bằng xét dấu nhị thức bậc nhất .
giải bất phương trình : \(\frac{x+2}{3x+1}\)<= \(\frac{x-2}{2x-1}\)
giải bằng xét dấu nhị thức bậc nhất
giải bất phương trình : \(\frac{x+2}{3x+1}\) <= \(\frac{x-2}{2x-1}\)
giải bằng xét dấu nhị thức bậc nhất
giải bất phương trình : \(\frac{x+2}{3x+1}\) <= \(\frac{x-2}{2x-1}\)
giải bằng xét dấu nhị thức bậc nhất
giải bất phương trình : \(\frac{x+2}{3x+1}\)<= \(\frac{x-2}{2x-1}\)
giải bằng xét dấu nhị thức bậc nhất
giải bất phương trình : \(\frac{x+2}{3x+1}\) <= \(\frac{x-2}{2x-1}\)
giải bằng xét dấu nhị thức bậc nhất
Giúp e câu c với ạ. Giải bất phương trình sử dụng dấu nhị thức bậc nhất
Do \(x^2+x+1=\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0;\forall x\) nên BPT tương đương:
\(-3\left(x^2+x+1\right)\le x^2-3x-1\le3\left(x^2+x+1\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-3x-1\ge-3x^2-3x-3\\x^2-3x-1\le3x^2+3x+3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}4x^2\ge-2\left(luôn-đúng\right)\\2x^2+6x+4\ge0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x\ge-1\\x\le-2\end{matrix}\right.\)
Phát biểu quy tắc xét dấu một nhị thức bậc nhất. Áp dụng quy tắc đó để giải bất phương trình :
\(\dfrac{\left(3x-2\right)\left(5-x\right)}{\left(2-7x\right)}\ge0\)
Quy tắc xét dấu một nhị thức dựa trên định lí :
“Nhị thức f(x) = ax + b (a≠0) có dấu cùng với hệ số a khi x lấy giá trị trong khoảng (−ba,+∞)(−ba,+∞) và trái dấu với hệ số a khi x lấy các giá trị thuộc khoảng (−∞,−ba)(−∞,−ba)”.
Áp dụng: Ta lập bảng xét dấu của vế trái f(x) của bất phương trình:
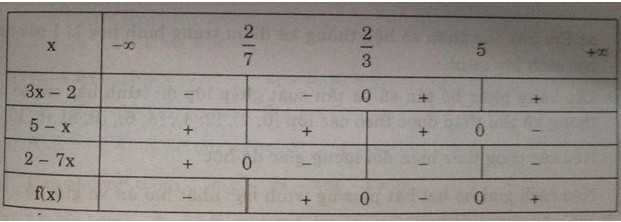
Tập nghiệm của bất phương trình: S=(27,23]∪[5,+∞)
giải bất phương trình bằng cách xét dấu nhị thức bâc nhất :
a) (2 + x ).(5 - x) > = 0
b)(2x -1).(3x-4)>= 0
Cái này sử dụng bảng xét dấu cho nhanh nhá !
\(a,\left(2+x\right)\left(5-x\right)\ge0\)
Ta có bảng xét dấu :
=> -2 \(\le x\le5\)
b) \(\left(2x-1\right)\left(3x-4\right)\ge0\)
=> 1/2 \(\le x\) hoặc x \(\ge\dfrac{4}{3}\)