Ta co:

Vì tam ABC vuông tại A co D là trung điểm BC nên \(\widehat{MAC}=\widehat{MCA}=\frac{\widehat{AMB}}{2}\)

\(\Rightarrow\beta=2\alpha\)

Từ đây ta co:

\(cos^2\alpha-sin^2\alpha=cos\left(2\alpha\right)=cos\beta\)

Bài giải ở trên đo

Ah chăc câu này ghi nhầm đề nên ghi lại câu kia đung không. Thôi xem câu trên đi

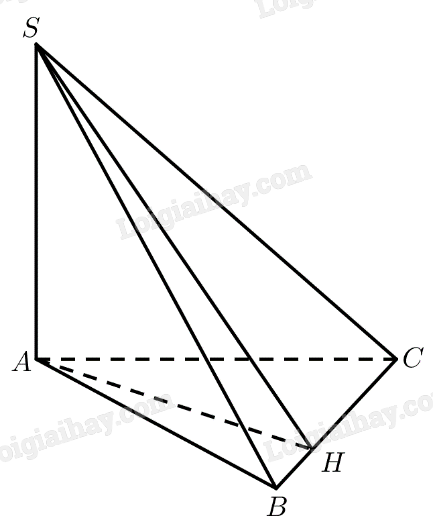
Kẻ \(AH \bot BC\left( {H \in BC} \right)\)

\(SA \bot \left( {ABC} \right) \Rightarrow SA \bot BC\)

\( \Rightarrow BC \bot \left( {SAH} \right) \Rightarrow BC \bot SH\)

Vậy \(\widehat {SHA}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {A,BC,S} \right]\)

\( \Rightarrow \widehat {SHA} = \alpha \)

\(\begin{array}{l}{S_{\Delta ABC}} = \frac{1}{2}BC.AH,{S_{\Delta SBC}} = \frac{1}{2}BC.SH\\ \Rightarrow \frac{{{S_{\Delta ABC}}}}{{{S_{\Delta SBC}}}} = \frac{{\frac{1}{2}BC.AH}}{{\frac{1}{2}BC.SH}} = \frac{{AH}}{{SH}} = \cos \widehat {SHA} = \cos \alpha \end{array}\)

\(SABC=\frac{1}{2}BH\cdot AC\)

ma trong tam giac vuong BHC co \(BH=AB\cdot sinalpha\)

suy ra dien h tam giac ABC =\(\frac{1}{2}AB\cdot AC\cdot sinalpha\) mới đúng bạn ạ

tam giác này vuông ở đâu z bạn???????

Ta có : \(\left(sin\alpha+cos\alpha\right)^2=sin^2\alpha+cos^2\alpha+2sin\alpha.cos\alpha\) (1)

Lại có : \(sin^2\alpha=\frac{AB^2}{BC^2}\) ; \(cos^2\alpha=\frac{AC^2}{BC^2}\) \(\Rightarrow sin^2\alpha+cos^2\alpha=\frac{AB^2+AC^2}{BC^2}=\frac{BC^2}{BC^2}=1\) (2)

Kẻ đường cao AH (H thuộc BC)

Ta sẽ chứng minh \(sin\beta=2sin\alpha.cos\alpha\)

Xét tam giác vuông HMA có : \(sin\beta=\frac{AH}{AM}\) 

Lại có \(AH=\frac{AB.AC}{BC}\) ; \(AM=\frac{BC}{2}\) \(\Rightarrow sin\beta=\frac{\frac{AB.AC}{BC}}{\frac{BC}{2}}=\frac{2AB.AC}{BC^2}=2.\frac{AB}{BC}.\frac{AC}{BC}=2sin\alpha.cos\alpha\)(3)

Từ (1) , (2) , (3) ta có điều phải chứng minh.