Tìm điều kiện xác định của mỗi biểu thức sau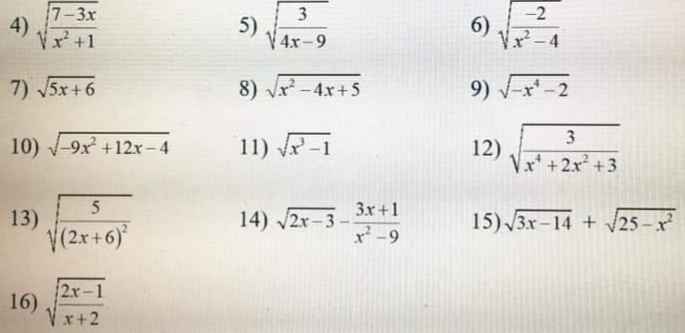

Những câu hỏi liên quan
Đối với mỗi biểu thức sau, hãy tìm điều kiện của x để giá trị của biểu thức được xác định: 2 x 2 + 1 x x - 1
Biểu thức 2 x 2 + 1 x x - 1 xác định khi: x ≠ 0 và x – 1 ≠ 0 ⇔ x ≠ 0 và x ≠ 1
Vậy điều kiện để biểu thức xác định là x ≠ 0 và x ≠ 1.
Đúng 0
Bình luận (0)
Đối với mỗi biểu thức sau, hãy tìm điều kiện của x để giá trị của biểu thức được xác định: 2 x - 3 x - 1 x + 2
Biểu thức 2 x - 3 x - 1 x + 2 xác định khi:
x – 1 ≠ 0 và x + 2 ≠ 0 ⇔ x ≠ 1và x ≠ - 2
Vậy điều kiện để biểu thức xác định là x ≠ 1 và x ≠ - 2.
Đúng 0
Bình luận (0)
Đối với mỗi biểu thức sau, hãy tìm điều kiện của x để giá trị của biểu thức được xác định: x 2 - 25 x 2 - 10 x + 25 x
Biểu thức x 2 - 25 x 2 - 10 x + 25 x xác định khi x 2 - 10 x + 25 ≠ 0 và x ≠ 0
x 2 - 10 x + 25 ≠ 0 ⇔ x - 5 2 ≠ 0 ⇔ x ≠ 5
Vậy điều kiện để biểu thức xác định là x ≠ 0 và x ≠ 5
Đúng 0
Bình luận (0)
Đối với mỗi biểu thức sau, hãy tìm điều kiện của x để giá trị của biểu thức được xác định:
x
2
-
25
x
2
+
10
x
+
25
x
-
5
Đọc tiếp
Đối với mỗi biểu thức sau, hãy tìm điều kiện của x để giá trị của biểu thức được xác định: x 2 - 25 x 2 + 10 x + 25 x - 5
Biểu thức x 2 - 25 x 2 + 10 x + 25 x - 5 xác định khi x 2 + 10 x + 25 ≠ 0 và x - 5 ≠ 0
x 2 + 10 x + 25 ≠ 0 ⇔ x + 5 2 ≠ 0 ⇔ x ≠ - 5
x – 5 ≠ 0 ⇔ x ≠ 5
Vậy điều kiện để biểu thức xác định là x ≠ 5 và x ≠ - 5.
Đúng 0
Bình luận (0)
 chỉ cần b2: tìm điều kiện xác định của mỗi biểu thức là đc ạ
chỉ cần b2: tìm điều kiện xác định của mỗi biểu thức là đc ạ
Bài 3:
a: \(A=\dfrac{x^2+x-2-x^2+x-2}{\left(x+1\right)^2\left(x-1\right)}\cdot\dfrac{\left(x+1\right)^2\left(x-1\right)}{x\left(2x+1\right)}\)
\(=\dfrac{2}{2x+1}\)
Đúng 0
Bình luận (0)
Bài 3:
\(a,ĐK:x\ne\pm1;x\ne0;x\ne-\dfrac{1}{2}\\ A=\dfrac{x^2+x-2-x^2+x+2}{\left(x+1\right)^2\left(x-1\right)}\cdot\dfrac{\left(x-1\right)\left(x+1\right)^2}{x\left(2x+1\right)}\\ A=\dfrac{2x}{x\left(2x+1\right)}=\dfrac{2}{2x+1}\\ b,x=-3\Leftrightarrow A=\dfrac{2}{-6+1}=-\dfrac{2}{5}\\ x=\dfrac{1}{4}\Leftrightarrow A=\dfrac{2}{\dfrac{1}{2}+1}=\dfrac{4}{3}\\ x=-\dfrac{1}{2}\Leftrightarrow A\in\varnothing\)
\(c,A=3\Leftrightarrow2x+1=\dfrac{2}{3}\Leftrightarrow x=-\dfrac{1}{6}\\ d,A=\dfrac{2}{3}\Leftrightarrow2x+1=3\Leftrightarrow x=1\)
Đúng 1
Bình luận (0)
Tìm điều kiện xác định của biến để giá trị của mỗi biểu thức sau xác định và chứng minh rằng với điều kiện đó biểu thức không phụ thuộc vào biến:
2/x-2 -2/x2 -x -2 .(1+3x+x2/x+3)
giúp mik với mik đang cần gấp :)))
Tìm điều kiện xác định của biểu thức sau
\(\sqrt{\dfrac{4}{2x-1}}\)
ĐK:`4/(2x-1)>=0(x ne 1/2)`
Mà `4>0`
`<=>2x-1>0`
`<=>2x>1`
`<=>x>1/2`
Vậy `x>1/2` thì `sqrt{4/(2x-1)}` có nghĩa
Đúng 3
Bình luận (0)
\(DK:\left\{{}\begin{matrix}2x-1>0\\4\ge2x-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x>\dfrac{1}{2}\\x\le\dfrac{5}{2}\end{matrix}\right.\)
Vậy \(x\in(\dfrac{1}{2};\dfrac{5}{2}]\) hay \(\dfrac{1}{2}< x\le\dfrac{5}{2}\)
Đúng 1
Bình luận (0)
Tìm điều kiện xác định của biểu thức sau:
\(\sqrt{x^2-4x+3}\)
đkxđ:
\(x^2-4x+3\ge0\)
\(\Leftrightarrow\left(x-1\right)\left(x-3\right)\ge0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x-1\ge0\\x-3\ge0\end{matrix}\right.\\\left\{{}\begin{matrix}x-1\le0\\x-3\le0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x\ge3\\x\le1\end{matrix}\right.\)
Vậy đkxđ của biểu thức là \(\left[{}\begin{matrix}x\ge3\\x\le1\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Tìm điều kiện xác định cảu biểu thức sau
\(\sqrt{2x+3}\)
\(2x+3\ge0\)
\(\Leftrightarrow x\ge\dfrac{-3}{2}\)
Đúng 1
Bình luận (0)





















