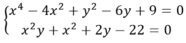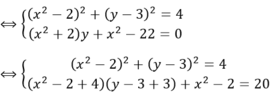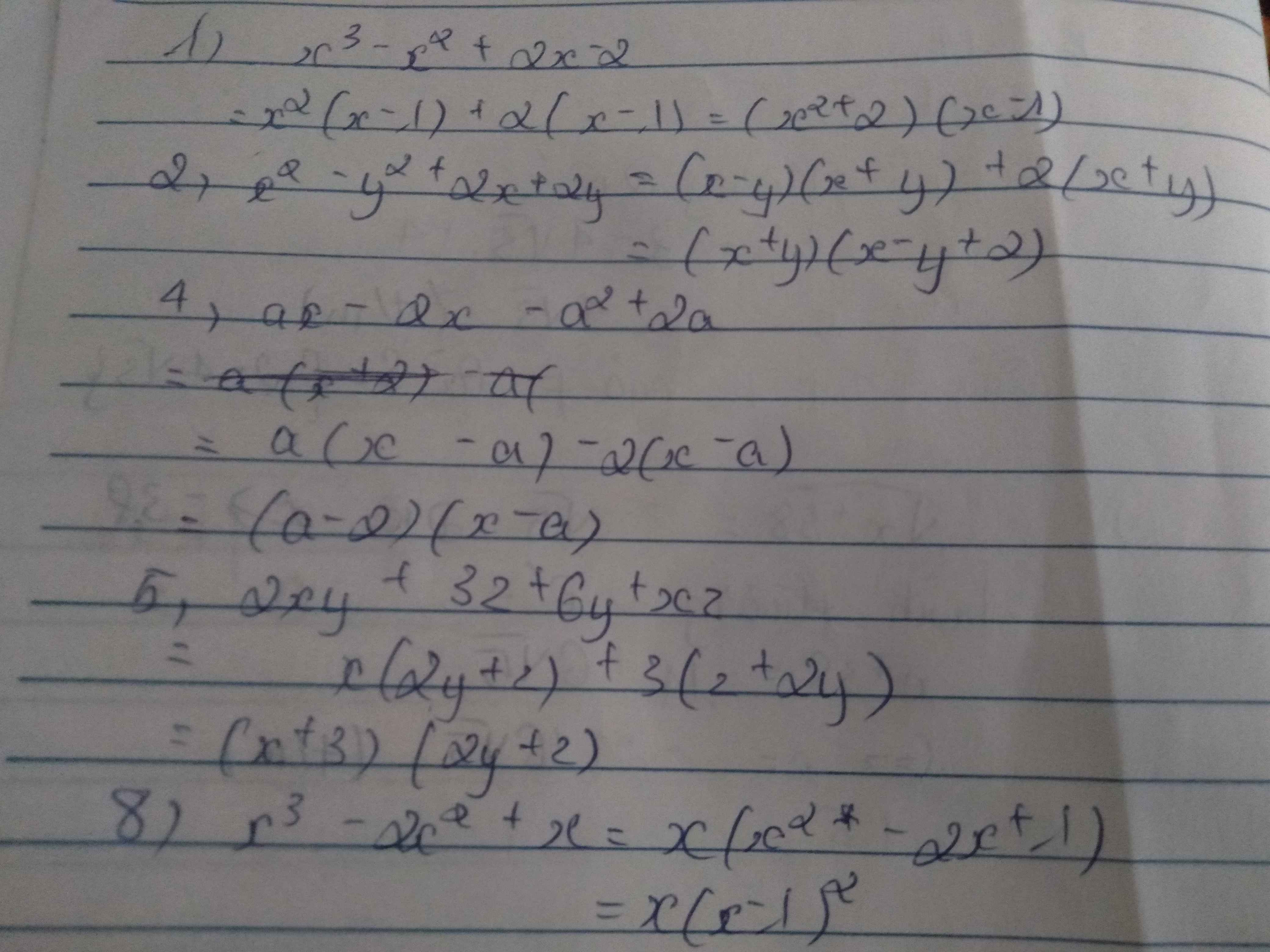x2+6y+9-y2

Những câu hỏi liên quan
Phân tích các đa thức sau thành nhân tử:a) 2xy + 3z + 6y + xz; b)
a
4
-
9
a
3
+
a
2
- 9a;c) 3
x
2
+ 5y - 3xy + (-5x); d)
x
2
- (a + b)x + ab;e) 4
x
2
- 4xy + ...
Đọc tiếp
Phân tích các đa thức sau thành nhân tử:
a) 2xy + 3z + 6y + xz; b) a 4 - 9 a 3 + a 2 - 9a;
c) 3 x 2 + 5y - 3xy + (-5x); d) x 2 - (a + b)x + ab;
e) 4 x 2 - 4xy + y 2 - 9 t 2 ; g) x 3 – 3 x 2 y + 3x y 2 – y 3 – z 3
h) x2 - y2 + 8x + 6y + 7.
a) Cách 1.
Ta có 2xy + 3z + 6y + xz = (2xy + xz) + (3z + 6y)
= x(2 y + z)+3(z + 2 y) = (z + 2y)(x + 3).
Cách 2.
Ta có 2xy + 3z + 6y + xz = (2x1/ + 6y) + (3z + xz)
= 2y(x + 3) + z(3 + x) = (z + 2y)(x + 3).
b) Biến đổi được a 4 - 9 rt 3 + a 2 -9a = (a- 9)a( a 2 +1).
c) Biến đổi được 3 x 2 + 5y - 3xy + (-5x) = (x - y)(3x - 5).
d) Biến đổi được x 2 - (a + b)x + ab = (x- a)(x - b).
e) Ta có 4 x 2 - 4xy + y 2 – 9 t 2 = ( 2 x - y ) 2 - ( 3 t ) 2
= (2x - y - 3t )(2x - y + 31).
g) Ta có x 3 - 3 x 2 y + 3 xy 2 - y 3 - z 3
= ( x - y ) 3 - z 3 = (x - y - z)( x 2 + y 2 + z 2 - 2xy + xz - yz).
h) Ta có x 2 - y 2 + 8x + 6y+ 7 = ( x 2 +8x + 16) - ( y 2 - 6y+ 9)
= ( x + 4 ) 2 - ( y - 3 ) 2 =(x-y + 7)(x + y + l).
Đúng 0
Bình luận (0)
Phân tích đa thức thành nhân tử:
a) 3(x-5)-x2+5x
b) 7x2-14xy+7y2
c) (x2+y2)2-4x2y2
d) -25x2+y2+9-6y
\(a,=3\left(x-5\right)-x\left(x-5\right)=\left(3-x\right)\left(x-5\right)\\ b,=7\left(x^2-2xy+y^2\right)=7\left(x-y\right)^2\\ c,=\left(x^2+y^2-2xy\right)\left(x^2+y^2+2xy\right)=\left(x-y\right)^2\left(x+y\right)^2\\ d,=\left(y^2-6y+9\right)-25x^2=\left(y-3\right)^2-25x^2=\left(y-5x-3\right)\left(y+5x-3\right)\)
Đúng 2
Bình luận (0)
Cho đường tròn (C) : x2+ y2+ 8x+ 6y+ 9 0. Mệnh đề nào sau đây sai? A. (C) không đi qua điểm O. B. tâm I( -4; -3). C.bán kính R 4. D. (C) đi qua điểm M(-1; 0) .
Đọc tiếp
Cho đường tròn (C) : x2+ y2+ 8x+ 6y+ 9= 0. Mệnh đề nào sau đây sai?
A. (C) không đi qua điểm O.
B. tâm I( -4; -3).
C.bán kính R= 4.
D. (C) đi qua điểm M(-1; 0) .
+Ta có a= -4; b= -3 ; c= 9 và a2+ b2- c= 16+ 9 - 9 = 16> 0
Suy ra (C) là đường tròn tâm I( -4; -3) và R= 4
Vậy B; C đúng.
+Thay O vào (C) ta có: 02+ 02+ 8.0+ 6.0 + 9= 0 vô lí . Vậy A đúng.
+Thay M( -1; 0) vào (C) ta có: (-1) 2+ 02+ 8.(-1) + 6.0 + 9= 0 ( vô lý). Vậy D sai.
Chọn D.
Đúng 0
Bình luận (0)
Số nghiệm của hệ phương trình
x
4
-
4
x
2
+
y
2
-
6
y
+
9...
Đọc tiếp
Số nghiệm của hệ phương trình x 4 - 4 x 2 + y 2 - 6 y + 9 = 0 x 2 y + x 2 + 2 y - 22 = 0 là:
A. 4
B. 1
C. 2
D. 3
Tìm giá trị lớn nhất:
A = -(2x - 5)2 + /2x - 5/ + 4.
B = -x2 - y2 + 2x - 6y + 9.
b: Ta có: \(B=-x^2-y^2+2x-6y+9\)
\(=-\left(x^2-2x+y^2+6y-9\right)\)
\(=-\left(x^2-2x+1+y^2+6y+9-19\right)\)
\(=-\left(x-1\right)^2-\left(y+3\right)^2+19\le19\forall x,y\)
Dấu '=' xảy ra khi x=1 và y=-3
Đúng 0
Bình luận (0)
Phân tích đa thức x2 - y2 + 6y - 9 thành nhân tử , ta được kết quả là cứu em
Phân tích đa thức thành nhân tử:
+)5x2y2+15x2+30xy2
+)(x-2)(x-3)+4-x2
+)x2-7x+12
+)x3-2x2y+xy2-9x
+)x2-25+y2+2xy
+)x2-x-12
+)5x25xy-x-y
+)12y(2x-5)+6xy(5-2x)
+)16x2+24x-8xy-6y+y2
+)(x+3)(x+6)(x+9)(x+12)+81
a: \(=5x\left(xy^2+3x+6y^2\right)\)
b: \(=\left(x-2\right)\left(x+3\right)-\left(x-2\right)\left(x+2\right)=\left(x-2\right)\left(x+3-x-2\right)=\left(x-2\right)\)
c: \(=\left(x-3\right)\left(x-4\right)\)
d: \(=x\left(x^2-2xy+y^2-9\right)\)
=x(x-y-3)(x-y+3)
e: \(=\left(x+y\right)^2-25=\left(x+y+5\right)\left(x+y-5\right)\)
f: \(=\left(x-4\right)\left(x+3\right)\)
Đúng 0
Bình luận (0)
1) x3-x2+2x-2 4) ax-2x-a2+2a 7) x2-6xy-25z2+9y2
2) x2-y2+2x+2y 5) 2xy +3z+6y+xz 8) x3-2x2+x
3) x2/4+2xy+4y2-25 6) x2y2+yz+y3+zx2 9) x4+4
a) A = x2 - 2x + 1 - y2 + 2x - 1
b) A = x2 - 4x + 4 - y2 - 6y - 9
c) A = 4x2 - 4x + 1 - y2 - 8y - 16
d) A = x2 - 2xy + y2 - z2 + zt - t2
a) A = x2 - 2x + 1 - y2 + 2x - 1
= (x2 - 2x + 1)-( y2-2x+1)
= (x-1)2-(y-1)2
= (x-1-y+1)(x-1+y-1)
b) A = x2 - 4x + 4 - y2 - 6y - 9
= (x2 - 4x + 4)-(y2+6y+9)
= (x-2)2-(y+3)2
= (x-2-y-3)(x-2+y+3)
c) A = 4x2 - 4x + 1 - y2 - 8y - 16
= (4x2 - 4x + 1) - (y2+8y+16)
= (2x-1)2-(y+4)2
= (2x-1-y-4)(2x-1+y+4)
d) A = x2 - 2xy + y2 - z2 + 2zt - t2
=(x2 - 2xy + y2)-(z2- 2zt + t2)
= (x-y)2-(z-t)2
=(x-y-z+t)(z-y+z-t)
câu d mik có sửa lại đề vì mik thấy đề hơi sai
Đúng 1
Bình luận (0)
a) A =
= x2 - y2 + 2x - 2x + 1 - 1
= x2 - y2 = (x-y) (x+y)
b) A=
= (x-2)2 - (y+3)2 = (x-y-5) (x+y+1)
c) A=
= (2x-1)2 - (y+4)2
= (2x+y+3) (2x-y-5)
d) đề có thể sai
Đúng 1
Bình luận (0)