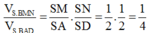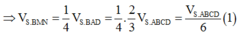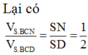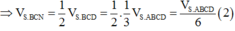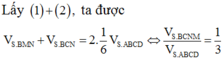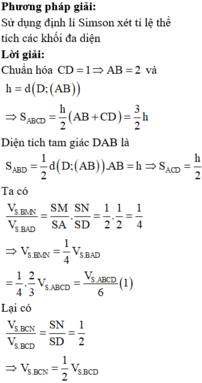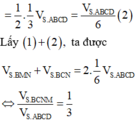Cho hình thang ABCD có 2CD=3AB .Gọi M trung điểm của AB ; P, N là hai điểm thuộc CD sao cho CN=NP=PD .Chứng minh
a, AMPD là hình bình hành
b, MC đi qua trung điểm của BN
c, MN,BP cắt nhau tại trung điểm của mỗi đường

Những câu hỏi liên quan
Cho hình thang ABCD có 2CD=3AB .Gọi M trung điểm của AB ; P,N là hai điểm thuộc CD sao cho CN=NP=PD .Chứng minh
a, AMPD là hình bình hành
b, MC đi qua trung điểm của BN
c, MN,BP cắt nhau tại trung điểm của mỗi đường
a) Ta có: M là trung điểm của AB(gt)
nên \(AM=MB=\dfrac{AB}{2}\)
Ta có: DP=PN=NC
mà DP+PN+NC=DC(gt)
nên \(DP=PN=NC=\dfrac{DC}{3}\)(1)
Ta có: \(2CD=3AB\)
nên \(AB=\dfrac{2}{3}CD\)
mà \(AM=\dfrac{1}{2}AB\)
nên \(2AM=\dfrac{2}{3}CD\)
hay \(AM=\dfrac{1}{3}CD\)(2)
Từ (1) và (2) suy ra AM=DP
Xét tứ giác AMPD có
AM//DP
AM=DP
Do đó: AMPD là hình bình hành
Đúng 1
Bình luận (0)
b) Xét tứ giác MBCN có
MB//NC
MB=NC
Do đó: MBCN là hình bình hành
Suy ra: Hai đường chéo MC và BN cắt nhau tại trung điểm của mỗi đường(đpcm)
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình thang, AB//CD, AB2CD. Gọi M N, tương ứng là trung điểm của SA và SD. Tính tỉ số
V
S
.
B
C
N
M
V
S
.
B
C
D
A
Đọc tiếp
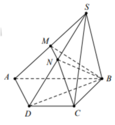
Cho hình chóp S.ABCD có đáy ABCD là hình thang, AB//CD, AB=2CD. Gọi M N, tương ứng là trung điểm của SA và SD. Tính tỉ số V S . B C N M V S . B C D A
![]()
Cho hình chóp S.ABCD có đáy ABCD là hình thang,
A
B
/
/
C
D
,
A
B
2
C
D
.
Gọi M N, tương ứng là trung điểm của SA và SD. Tính tỉ số
V
S
.
B
C
N
M
V
S...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thang, A B / / C D , A B =2 C D . Gọi M N, tương ứng là trung điểm của SA và SD. Tính tỉ số V S . B C N M V S . B C D A
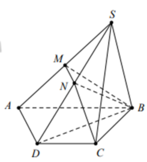
A. 5 12
B. 3 8
C. 1 3
D. 1 4
cho hình thang abcd(ab//cd)có ab=ad=1/2cd . gọi m là trung điểm cua cd. gọi h là giao điểm của am và bd. chứng minh tứ giác abmd là hình thoi
Cho hình thang vuông ABCD A=D=90 . có AB=1/2CD . Gọi H là hình chiếu của D trên AC . M là trung điểm của HC . Chứng minh rằng :
góc BMD=90
Gọi N là trung điểm của HD .
Ta có : MN là đường trung bình của tam giác HDC
\(\Rightarrow MN//DC\)
\(MN=\frac{1}{2}DC\) (T/c đường TB )
Ta lại có :
\(AB//DC\)và \(AB=MN\)
=> ABMN là hình bình hành .
\(\Rightarrow AN//BM\)(1)
Xét tam giác ADM có :
\(\hept{\begin{cases}DH\perp AM\\MN\perp AD\end{cases}}\)
\(\Rightarrow AN\perp DM\)(2)
Từ (1) và (2)
\(\Rightarrow\widehat{BMD}=90^o\)(đpcm)
Đúng 0
Bình luận (0)
bn ơi dựa vào đâu để MN vuông góc AD trong tam giác ADM
Đúng 1
Bình luận (0)
Cho hình thang ABCD có AB//CD và AB=1/2CD. Gọi E là trung điểm của cạnh CD. Chứng minh các tứ giác ABED,ABCE là các hình bình hành
Ta có: \(AB=\dfrac{1}{2}CD\)(gt)
mà \(ED=EC=\dfrac{CD}{2}\)(E là trung điểm của CD)
nên AB=ED=EC
Xét tứ giác ABED có
AB//DE
AB=DE(cmt)
Do đó: ABED là hình bình hành
Xét tứ giác ABCE có
AB//CE
AB=CE
Do đó: ABCE là hình bình hành
Đúng 0
Bình luận (0)
- Do E là trung điểm của CD
\(=>DE=CE=\dfrac{CD}{2}\)
Mà \(AB=\dfrac{1}{2}CD\) (gt)
\(=>AB=DE=CD\)
- DE và CE trùng CD, AB // CD => AB // DE // CE
Tứ giác ABED có:
- AB=DE (cmt)
- AB // DE (cmt)
Vậy: Tứ giác ABED là hình bình hành (đpcm)
- Tương tự: Tứ giác ABCE có
- AB=CE (cmt)
- AB // CE (cmt)
Vậy tứ giác ABCE là hình bình hành (đpcm)
Đúng 0
Bình luận (0)
Cho hình thang ABCD có AB//CD và AB=1/2CD. Gọi E là trung điểm của CD. CM tứ giác ABED, ABCE là hình bình hành
helpp
Cho hình thang vuông ABCD. Góc A=góc D= 90 độ, AB =1/2CD. Gọi H là hình chiếu của D trên AC. M là trung điểm HC. C/M: góc BMD=90 độ
cho hình thang cân abcd (ab//cd) có ab=2ad=2cd=2bc gọi p là đường trung bình ad q là đường trung bình bc c/m bd>pq