a: Xet ΔBAD vuông tại A và ΔBED vuông tại E có

BD chung

góc ABD=góc EBD

=>ΔBAD=ΔBED

=>BA=BE và DA=DE

=>BD là trung trựccủa AE

b: Xét ΔDAF vuông tại A và ΔDEC vuông tại E có

DA=DE

góc ADF=gócEDC

=>ΔDAF=ΔDEC

=>DF=DC

c: AD=DE
mà DE<DC

nên AD<DC

d: Xet ΔBFC có BA/AF=BE/EC

nên AE//CF

a:Xét ΔBAD vuông tại A và ΔBED vuông tại E có

BD chung

góc ABD=góc EBD

=>ΔBAD=ΔBED

=>BA=BE và DA=DE

=>BD là trung trực của AE

b: Xét ΔDAF vuông tại A và ΔDEC vuông tại E có

DA=DE

góc ADF=góc EDC

=>ΔDAF=ΔDEC

=>DF=DC

c: AD=DE

DE<DC

=>AD<DC

(a) Xét \(\Delta ABD,\Delta EBD:\left\{{}\begin{matrix}\hat{BAD}=\hat{BED}=90^o\left(gt\right)\\\text{BD chung}\\\hat{EBD}=\hat{ABD}\left(gt\right)\end{matrix}\right.\)

\(\Rightarrow\Delta ABD=\Delta EBD\left(c.h-g.n\right)\Rightarrow\left\{{}\begin{matrix}BA=BE\\DA=DE\end{matrix}\right.\)

\(\Rightarrow BD\) là đường trung trực của \(AE\left(đpcm\right).\)

(b) Xét \(\Delta ADF,\Delta EDC:\left\{{}\begin{matrix}\hat{DAF}=\hat{DEC}=90^o\left(gt\right)\\AD=DE\left(cmt\right)\\\hat{ADF}=\hat{EDC}\left(\text{đối đỉnh}\right)\end{matrix}\right.\)

\(\Rightarrow\Delta ADF=\Delta EDC\left(g.c.g\right)\Rightarrow AF=CE.\)

Lại có: \(BA=BE\left(cmt\right)\Rightarrow BA+AF=BE+CE\Leftrightarrow BC=BF\)

\(\Rightarrow\Delta BCF\) cân tại \(B.\)

Ta cũng có: \(\left\{{}\begin{matrix}FE\perp BC\\CA\perp BF\\FE\cap CA=\left\{D\right\}\end{matrix}\right.\Rightarrow BD\) là đường cao thứ ba của \(\Delta BCF\Rightarrow BD\) vừa là đường cao, vừa là đường trung trực của \(CF\Rightarrow DC=DF\left(đpcm\right).\)

Ta có tan giác BAD=tam giác BED(ch-gn)

                    =>BA=BE (tương ứng)

Vậy B cach đều hai đều mút của đoạn thẳng AE 

=>BD là trung trực của AE 

b)Từ a có tam giác BAD=BED 

                            =>AD=DE(tương ứng)

Vậy ta có tam giác ADF=EDC (cgv-gnk)

=>DC=DF(tương ứng)

c) trong tam giac vuông ADF có AD< DF(vì FD là cạnh huyền và là cạnh lớn nhất trong tam giác vuông)

Mà theo câu b ta có DF=DC 

NÊN => AD<DC

=> 

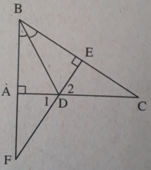
Xét ΔABD và ΔEBD có:

BD chung

∠ABD = ∠EBD ( do BD ,là tia phân giác của góc ABC )

∠BAD = ∠BED = 90º

Suy ra: ΔABD = ΔEBD (cạnh huyền – góc nhọn) ⇒ BA = BE, DA = DE.

Do BA = BE nên B thuộc đường trung trực của AE.

Do DA = DE nên D thuộc đường trung trực của AE.

Do đó BD là đường trung trực của AE.

a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có

BD chung

góc ABD=góc EBD

=>ΔBAD=ΔBED

b: BA=BE

DA=DE

=>BD là trung trực của AE

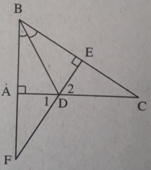
Xét ΔDAF và ΔDEC có:

DA = DE( chứng minh trên)

∠D1 = ∠D2 ( hai góc đối đỉnh)

∠DAF = ∠DEC = 90º

Suy ra: ΔDAF = ΔDEC (g.c.g) ⇒ DF = DC.