a) Giải BPT: 3x^3-5x^2-x-2>0
b)Tìm min của A=2x^2+y^2-2xy-2x+3
f(x)=(2x-3)^2+(x+4)^2-(3x^2+5x-2) tìm GTNN
F=2x^2+3y^2-8x+24y-7 tìm GTNN
F=-5x^2-4y^2+20x-32y+9 tìm GTLN
F=x^2+y^2-x+y-3 tìm GTNN
F=F=5x^2+y^2-4xy-6x+20 tìm GTNN
F=-13x^2-4y^2+12xy+20x+37
F=5x^2+9y^2-12xy+24x-48y+100
Cho x+y=5 Cho A= x^3+y^3-8(x^2+y^2)+xy+2 tính GTLN của A
Cho x+y+2=0 Tìm min của B=2(x^3+y^3)-15xy+7
Cho x+y+2=0 tìm min của C=x^4+y^4-(x^3+y^3)+2x^2y^2+2xy(x^2+y^2)+13xy
Bài 1:
a) 7x –12 = 5x + 3
b) 2(3x –5) –7(x + 1) = 2
c) (1 –3x)^2= (4x –3)^2
d) (2x + 3)(4x –2) –2(2x + 1)^2= 12
Bài 2:
Cho biểu thứcA = (5x –3y + 1)(7x + 2y –2)
a) Tìm x sao cho với y = 2 thì A = 0
b) Tìm y sao cho với x = -2 thì A = 0
1.
a.\(\Leftrightarrow7x-5x=3+12\)
\(\Leftrightarrow2x=15\Leftrightarrow x=\dfrac{15}{2}\)
b.\(\Leftrightarrow6x-10-7x-7=2\)
\(\Leftrightarrow x=-19\)
c.\(\Leftrightarrow1-3x=4x-3\)
\(\Leftrightarrow7x=2\Leftrightarrow x=\dfrac{2}{7}\)
d.\(\Leftrightarrow8x^2-4x+12x-6-8x^2-8x-2=12\)
\(\Leftrightarrow-2=12\left(voli\right)\)
Bài 1: Phân tích đa thức sau :
a)2x(xy+y^2-3)
b)(x-y)(2x+y)
c)(x-2y)^2
d)(2x-y)(y+2x)
bài 2: Phân tích các đơn thức thành nhân tử
a)3x^2-3xy
b)x^2-4y^2
c)3x-3y+xy-y^2
d)x^2-1+2y-y^2
Bài 3: Tìm x biết:
a)3x^2-6x=0
b)Tìm x,y thuộc z biết: x^2+4y^2-2xy=4
Bài 2:
a: \(3x^2-3xy=3x\left(x-y\right)\)
b: \(x^2-4y^2=\left(x-2y\right)\left(x+2y\right)\)
c: \(3x-3y+xy-y^2=\left(x-y\right)\left(3+y\right)\)
d: \(x^2-y^2+2y-1=\left(x-y+1\right)\left(x+y-1\right)\)
1. Tìm Min
a, 3x^2 + 5x
b, (2x-1)^2 - x^2
2.Cho x+y=2. Tìm Min A = x^2+y^2
3. tìm Min A = x^2 + 6y^2 + 4xy - 2x - 8y + 2016
tìm x biết
a x^2 (2x+15)+4(2x+15)=0
b 5x(x-2)-3(x-2)=0
c 2(x+3)-x^2-3x=0
a
\(x^2\left(2x+15\right)+4\left(2x+15\right)=0\\ \Leftrightarrow\left(2x+15\right)\left(x^2+4\right)=0\\ \Leftrightarrow2x+15=0\left(x^2+4>0\forall x\right)\\ \Leftrightarrow2x=-15\\ \Leftrightarrow x=-\dfrac{15}{2}\)
b
\(5x\left(x-2\right)-3\left(x-2\right)=0\\ \Leftrightarrow\left(x-2\right)\left(5x-3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-2=0\\5x-3=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=0+2=2\\x=\dfrac{0+3}{5}=\dfrac{3}{5}\end{matrix}\right.\)
c
\(2\left(x+3\right)-x^2-3x=0\\ \Leftrightarrow2\left(x+3\right)-\left(x^2+3x\right)=0\\ \Leftrightarrow2\left(x+3\right)-x\left(x+3\right)=0\\ \Leftrightarrow\left(x+3\right)\left(2-x\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x+3=0\\2-x=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=0-3=-3\\x=2-0=2\end{matrix}\right.\)
a: =>(2x+15)(x^2+4)=0
=>2x+15=0
=>2x=-15
=>x=-15/2
b; =>(x-2)(5x-3)=0
=>x=2 hoặc x=3/5
c: =>(x+3)(2-x)=0
=>x=2 hoặc x=-3
Tìm x biết:
a) (2x - 3).(x + 5) = 0
b) 3x.(x - 2) - 7.(x - 2) = 0
c) 5x.(2x - 3) - 6x + 9 = 0
a)(2x-3)(x+5)=0
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=0\\x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=-5\end{matrix}\right.\)
Vậy x=3/2 hoặc x=-5
a) \(\left(2x-3\right)\left(x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=0\\x+5=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=-5\end{matrix}\right.\)
Vậy phương trình có tập nghiệm là: \(S=\left\{\dfrac{3}{2};-5\right\}\)
b) \(3x\left(x-2\right)-7\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(3x-7\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\3x-7=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=\dfrac{7}{2}\end{matrix}\right.\)
Vậy phương trình có tập nghiệm là: \(S=\left\{2;\dfrac{7}{2}\right\}\)
c) \(5x\left(2x-3\right)-6x+9=0\)
\(\Leftrightarrow5x\left(2x-3\right)-3\left(2x-3\right)=0\)
\(\Leftrightarrow\left(2x-3\right)\left(5x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=0\\5x-3=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=\dfrac{3}{5}\end{matrix}\right.\)
Vậy phương trình có tập nghiệm là: \(S=\left\{\dfrac{3}{2};\dfrac{3}{5}\right\}\)
a: Ta có: \(\left(2x-3\right)\left(x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=-5\end{matrix}\right.\)
b: Ta có: \(3x\left(x-2\right)-7\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(3x-7\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=\dfrac{7}{3}\end{matrix}\right.\)
c: Ta có: \(5x\left(2x-3\right)-6x+9=0\)
\(\Leftrightarrow\left(2x-3\right)\left(5x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=\dfrac{3}{5}\end{matrix}\right.\)
Tìm max hoặc min của A= -2x^2-8x+1
B=3x^2+3x-1
C=7x-2x^2+3
D=-4xy+4x-y^2-5x^2+3
\(B=3x^2+3x-1\)
\(=3\left(x^2+x-\dfrac{1}{3}\right)\)
\(=3\left(x^2+x+\dfrac{1}{4}-\dfrac{7}{12}\right)\)
\(=3\left(x+\dfrac{1}{2}\right)^2-\dfrac{7}{4}>=-\dfrac{7}{4}\forall x\)
Dấu '=' xảy ra khi x+1/2=0
=>\(x=-\dfrac{1}{2}\)
\(C=-2x^2+7x+3\)
\(=-2\left(x^2-\dfrac{7}{2}x-\dfrac{3}{2}\right)\)
\(=-2\left(x^2-2\cdot x\cdot\dfrac{7}{4}+\dfrac{49}{16}-\dfrac{73}{16}\right)\)
\(=-2\left(x-\dfrac{7}{4}\right)^2+\dfrac{73}{8}< =\dfrac{73}{8}\forall x\)
Dấu '=' xảy ra khi x-7/4=0
=>x=7/4
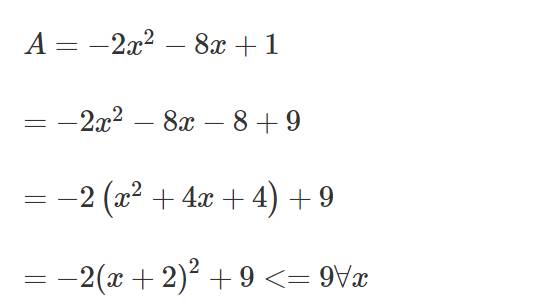
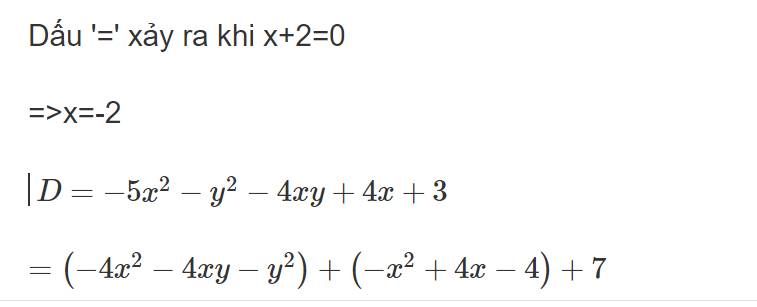
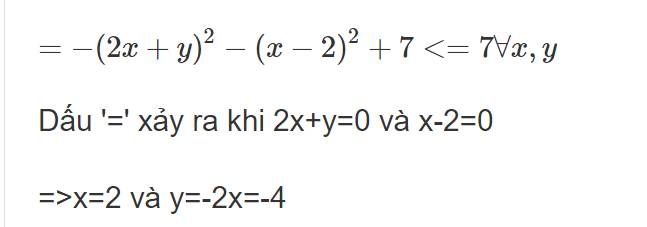
Bài 2 : Phân tích đa thức sau thành nhân tử
a) 5x^2 + 30y
b) x^3 - 2x^2 - 4xy^2 + x
Bài 3 : Tìm x , biết
a) 2x(x - 3 ) - x + 3 = 0
b) ( 3x - 1 ) ( 2x + 1 ) - (x + 1)^2 = 5x^2
Bài 2
a) 5x² + 30y
= 5(x² + 6y)
b) x³ - 2x² - 4xy² + x
= x(x² - 2x - 4y² + 1)
= x[(x² - 2x + 1) - 4y²]
= x[(x - 1)² - (2y)²]
= x(x - 1 - 2y)(x - 1 + 2y)
Bài 3:
a: \(2x\left(x-3\right)-x+3=0\)
=>\(2x\left(x-3\right)-\left(x-3\right)=0\)
=>(x-3)(2x-1)=0
=>\(\left[{}\begin{matrix}x-3=0\\2x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=\dfrac{1}{2}\end{matrix}\right.\)
b: \(\left(3x-1\right)\left(2x+1\right)-\left(x+1\right)^2=5x^2\)
=>\(6x^2+3x-2x-1-x^2-2x-1=5x^2\)
=>\(5x^2-x-2=5x^2\)
=>-x-2=0
=>-x=2
=>x=-2
Giải các phương trình sau
a. (2x-3)(x^2-4)=0
b. 2x-(3-5x)=4(x+3)
c. 1/x-2-2/x+1=11-3x/(x+1)(x-2)
\(a,\left(2x-3\right)\left(x^2-4\right)=0\\ \Leftrightarrow\left(2x-3\right)\left(x-2\right)\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=2\\x=-2\end{matrix}\right.\\ b,2x-\left(3-5x\right)=4\left(x+3\right)\\ \Leftrightarrow2x-3+5x=4x+12\\ \Leftrightarrow7x-3-4x-12=0\\ \Leftrightarrow3x-15=0\\ \Leftrightarrow x=5\)
\(c,ĐKXĐ:\left\{{}\begin{matrix}x\ne-1\\x\ne2\end{matrix}\right.\)
\(\dfrac{1}{x-2}-\dfrac{2}{x+1}=\dfrac{11-3x}{\left(x+1\right)\left(x-2\right)}\\ \Leftrightarrow\dfrac{x+1}{\left(x-2\right)\left(x+1\right)}-\dfrac{x-2}{\left(x+1\right)\left(x-2\right)}-\dfrac{11-3x}{\left(x+1\right)\left(x-2\right)}=0\\ \Leftrightarrow\dfrac{x+1-x+2-11+3x}{\left(x+1\right)\left(x-2\right)}=0\\ \Rightarrow3x-8=0\\ \Leftrightarrow x=\dfrac{8}{3}\left(tm\right)\)