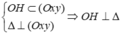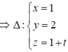Trong mặt phẳng toạ độ Oxy, cho (d) y=(m+5)x+2m-10. Tìm m để khoảng cách từ O đến d lớn nhất.

Những câu hỏi liên quan
Trong mặt phẳng toạ độ cho đường thẳng (d): y= (m+2)x+2m+3 .
a. Tìm m để (d) đi qua điểm A(2,5) .
b. Chứng minh rằng với mọi giá trị của tham số m thì (d) luôn đi qua một điểm cố định.
c. Tìm m để khoảng cách từ gốc O đến đường thẳng (d) là lớn nhất.
Trong mặt phẳng tọa độ Oxy, cho đường thẳng y=mx-3m+4 Tìm m để khoảng cách từ O đến đường thẳng (d) là lớn nhất. Tìm giá trị lớn nhất đó.
Trong mặt phẳng Oxy,cho đường thẳng `(d): (m-4)x+(m-3)y=1` (m là tham số).Tìm m để khoảng cách từ gốc tọa độ đến đường thẳng `(d)` là lớn nhất.
Xét m=4 =>(d):y=1 =>Khoảng cách từ gốc tọa độ đến đt (d) khi đó là 1
Xét m=3 =>(d):x=-1=> Khoảng cách từ gốc tọa độ đến đt (d) khi đó là 1
Xét \(m\ne4;m\ne3\)
Gọi \(A=Ox\cap\left(d\right)\) \(\Rightarrow A\left(\dfrac{1}{m-4};0\right)\), \(B=Oy\cap\left(d\right)\Rightarrow B\left(0;\dfrac{1}{m-3}\right)\)
Gọi H là hình chiếu của O lên AB
Có \(OH^2=\dfrac{OA^2.OB^2}{OA^2+OB^2}=\dfrac{\left(\dfrac{1}{m-4}\right)^2.\left(\dfrac{1}{m-3}\right)^2}{\left(\dfrac{1}{m-4}\right)^2+\left(\dfrac{1}{m-3}\right)^2}\)
\(=\dfrac{1}{\left(m-4\right)^2\left(m-3\right)^2\left[\dfrac{1}{\left(m-4\right)^2}+\dfrac{1}{\left(m-3\right)^2}\right]}\)
\(=\dfrac{1}{\left(m-4\right)^2+\left(m-3\right)^2}\)
\(=\dfrac{1}{2m^2-14m+25}=\dfrac{1}{2\left(m-\dfrac{7}{2}\right)^2+\dfrac{1}{2}}\le2\)
=> \(OH\le\sqrt{2}\)
=> Khoảng cách lớn nhất gốc tọa độ đến (d) là \(\sqrt{2}\Leftrightarrow m=\dfrac{7}{2}\) (thỏa)
Đúng 4
Bình luận (1)
Xét điểm \(A\left(-1;1\right)\). Dễ thấy A thuộc (d). Gọi H là hình chiếu của O trên (d). Ta có \(OH\le OA=\sqrt{2}\). Dấu "=" xảy ra khi và chỉ khi \(H\equiv A\), tức là \(d\perp OA\).
Ta cần tìm m sao cho \(d\perp OA\). Phương trình đường thẳng đi qua O, A là
y = -x. Xét m = 4 thì đường thẳng (d) trở thành \(y=1\), đường thẳng này song song với trục hoành và không vuông góc với d. Xét m khác 4. Khi đó \(\left(m-4\right)x+\left(m-3\right)y=1\Leftrightarrow y=\dfrac{4-m}{m-3}x+\dfrac{1}{m-3}\). Để \(d\perp OA\) thì \(\dfrac{4-m}{m-3}.\left(-1\right)=-1\Leftrightarrow4-m=m-3\Leftrightarrow m=\dfrac{7}{2}\).
Vậy Max \(OH=\sqrt{2}\Leftrightarrow m=\dfrac{7}{2}\).
Đúng 2
Bình luận (1)
Trên mặt phẳng tọa độ Oxy cho đương thẳng:
y=(2m+10)x-4m-1 và điểm A(-2;3).Tìm m để khoảng cách từ A đến đường thẳng trên là lớn nhất.
2mx -4m +10x -1 -y =0
2m(x-2) +(10x -1-y) =0
x =2 ; y =19 pt đúng với mọi m
=> h/s luôn qua điểm M(2;19) gọi K/c từ A đến d là AH
khoảng cách lờn nhất AH= AM ( AH </ AM)
khi đó AH vuông góc AM
+ gọi pt qua AM là y =ax +b => a =4 ; b =11
=>(2m+10) . 4 =-1
2m = -1/4 -10 =- 41/4
m =-41/8
Đúng 1
Bình luận (0)
khi đó am vuông góc với d nhé
tick cho mk nha bạn
Đúng 0
Bình luận (0)
Xác định m để khoảng cách từ điểm A( 3 ; 1 ) đến đường thẳng : x + ( m – 1)y + m = 0 là lớn nhất . Tìm giá trị lớn nhất đó
Đúng 0
Bình luận (0)
Trong mặt phẳng toạ độ Oxy,cho đường thẳng (d):y=2x+6
a):Viết phương trình đường thẳngđi qua M(3;4)váong song với đường thẳng (d)
b)Tính khoảng cách từ gốc toạ độ O đến đường thẳng (d)
Xem chi tiết
a) Gọi đường thẳng đi qua M(3;4) và song song với \(\left(d\right):y=2x+6\)là \(\left(d'\right):y=a'x+b'\)
Vì \(\left(d'\right)//\left(d\right)\Rightarrow a'=2\)
Vậy phương trình đường thẳng (d') có dạng \(\left(d'\right):y=2x+b'\)
Mặt khác (d') đi qua M(3;4) nên điểm M(3;4) thuộc \(\left(d'\right):y=2x+b'\)
Thay \(x=3;y=4\)vào hàm số \(y=2x+b'\)ta có:
\(4=2.3+b'\Leftrightarrow b'=-2\)
Vậy phương trình đường thẳng đi qua M(3;4) và song song với \(\left(d\right):y=2x+6\)là \(\left(d'\right):y=2x-2\)
b) Gọi OH là khoảng cách từ O đến (d). Gọi giao điểm của (d):y = 2x + 6 với hai trục Ox, Oy lần lượt là A(xA;0), B(0;yB).
Thay x = xA; y = 0 vào hàm số y = 2x + 6, ta có: \(0=2x_A+6\Leftrightarrow x_A=-3\)
Thay x = 0; y = yB vào hàm số y = 2x + 6, ta có: \(y_B=2.0+6=6\)
Vì \(OA=\left|x_A\right|;OB=\left|y_B\right|\)\(\Rightarrow OA=\left|-3\right|=3;OB=\left|6\right|=6\)
\(\Delta OAB\)vuông tại O, đường cao OH \(\Rightarrow\frac{1}{OH^2}=\frac{1}{OA^2}+\frac{1}{OB^2}\left(htl\right)\)
Rồi bạn thay OA, OB vào và dễ dàng tính được OH
Cho mặt phẳng Oxy ,cho đường thẳng (d) có phương trình (m-4)x+(m-3)y=1 (m là tham số). Tìm M để khoảng cách từ gốc tọa độ đến đường thẳng (d) là lớn nhất
a) Tính khoảng cách từ gốc toạ độ C(0;0) đến điểm M(3 ; 4) trong mặt phẳng toạ độ Oxy.
b) Cho hai điểm I(a; b) và M(x ; y) trong mặt phẳng toạ độ Oxy. Nêu công thức tính độ dài đoạn thẳng IM.
a) Khoảng cách từ gốc tọa độ \(O\left( {0;0} \right)\) đến điểm \(M\left( {3;4} \right)\) trong mặt phẳng tọa độ Oxy là:
\(OM = \left| {\overrightarrow {OM} } \right| = \sqrt {{3^2} + {4^2}} = 5\)
b) Với hai điểm I(a; b) và M(x ; y) trong mặt phẳng toạ độ Oxy, ta có:\(IM = \sqrt {{{\left( {x - a} \right)}^2} + {{\left( {y - b} \right)}^2}} \)
Đúng 0
Bình luận (0)
Trong không gian Oxyz, đường thẳng Δ qua điểm M(1−2m;2+ m;1) và vuông góc với mặt phẳng (Oxy) sao cho khoảng cách từ gốc toạ độ O đến đường thẳng Δ nhỏ nhất có phương trình là A.
x
1
y
2
z...
Đọc tiếp
Trong không gian Oxyz, đường thẳng Δ qua điểm M(1−2m;2+ m;1) và vuông góc với mặt phẳng (Oxy) sao cho khoảng cách từ gốc toạ độ O đến đường thẳng Δ nhỏ nhất có phương trình là
A. x = 1 y = 2 z = 1 + t
B. x = 1 + t y = 2 + t z = 1
C. x = 5 y = 0 z = 1 + t
D. x = 3 y = 1 z = 1 + t
trong mặt phẳng toạ độ Oxy cho (d): y = ( 2m-1 )x + 3m (m thuộc R)
a) tìm điểm cố định mà (d) luôn đi qua với mọi m
b) tính bán kính lớn nhất của ( o;r) sao cho đương tròn đó tiếp xúc (d)